Visibilité des planètes

(Planètes visibles entre les latitudes 60° Nord et 60° Sud et les constellations les plus voisines)

Mercure est visible vers l’est, le matin à l’aube avant le lever du Soleil jusqu’au 20 novembre, date de sa dernière visibilité du matin à Paris. Sa plus grande élongation ouest a lieu le 1er novembre. Elle est dans la constellation de la Vierge jusqu’au 13 novembre, date où elle entre dans la constellation de la Balance.

Vénus est invisible durant tout le mois de novembre.

Mars est visible au crépuscule et en début de nuit, au cours du mois elle se couche pratiquement toujours à la même heure. La planète est tout le mois dans la constellation du Sagittaire.

Jupiter est visible une très grande partie de la nuit et à l’aube. Au cours du mois, elle se lève de plus en plus tôt. Elle est tout le mois dans la constellation du Lion.

Saturne est invisible durant tout le mois de novembre, elle sera en conjonction le 18 novembre.

Aspect des planètes au 16 novembre 2014 Mercure, Vénus, Mars, Jupiter, Saturne, Uranus

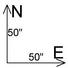
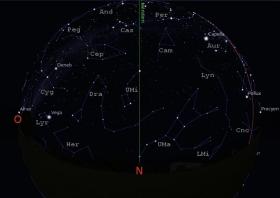
Ciel du mois

Cartes du ciel pour une observation vers le nord et vers le sud
à Paris le 15 novembre 2014 à 23 h temps légal

Carte du ciel en direction du nord	Carte du ciel en direction du sud

Ces cartes du ciel montrent les étoiles brillantes et les planètes visibles dans le ciel de l'hémisphère nord, vers l'horizon sud et vers l'horizon nord, pour le 15 novembre 2014 (23h). Le trait vertical correspond à la projection sur le ciel du méridien du lieu. L'arc de cercle rouge sur l'horizon sud représente l'écliptique (lieu de la trajectoire apparente du Soleil durant l'année). Les constellations visibles sur ces cartes sont, par ordre alphabétique des sigles :

Andromède (And), l'Aigle (Aql), le Verseau (Aqr), le Bélier (Ari), le Cocher (Aur), le Bouvier (Boo), la Girafe (Cam), Cassiopée (Cas), Céphée (Cep), la Baleine (Cet), le Cygne (Cyg), le Dauphin (Del), le Dragon (Dra), le Petit Cheval (Equ), Eridan (Eri), le Fourneau (For),les Gémeaux (Gem), Hercule (Her), le Lièvre (Lep), le Lézard (Lac),le Petit Lion (LMi), le Lynx (Lyn), la Lyre (Lyr), la Licorne (Mon), Pégase (Peg), Persée (Per), le Poisson (Psc), la Grande Ourse (UMa), la Petite Ourse (UMi), le Sculpteur (Scl), le Serpent (Ser), la Flèche (Sge), le Sagittaire (Sgr), le Triangle (Tri), le Petit Renard (Vul).

Le Soleil dans sa course apparente sur l'écliptique est accompagné de plusieurs planètes proches. Celles qui sont à l'est peuvent être observées au coucher du Soleil et au début de nuit selon leur élongation et leur magnitude, celles qui sont à l'ouest le seront en fin de nuit et au lever du Soleil sous les mêmes conditions. La figure suivante montre la configuration au 15 novembre 2014.

Les cartes du ciel sont générées à l'aide du logiciel libre Stellarium.

Nouvelles astronomiques

L'antenne de 26 m de diamètre de la station de Goldstone du Jet Propulsion Laboratory où fut détecté en temps réel le premier écho radar sur Vénus le 10 mars 1961.

Vers la fin des années cinquante, avec l'apparition de l'astronomie radar non passive liée aux exigences de précision astrométrique de la conquête spatiale, une nouvelle méthode va s'ouvrir pour déterminer l'unité astronomique – ou, ce qui revient au même, la parallaxe solaire - avec une précision inégalée. La cible : Vénus à sa conjonction inférieure. Commencée au MIT, la technologie et la méthode vont atteindre leur forme la plus aboutie avec le JPL et les grandes antennes de Goldstone.

La méthode des échos radar sur Vénus permet de mesurer la distance de la Terre à Vénus par mesure du temps d'aller-retour d'une onde radio envoyée sur Vénus. La connaissance de la vitesse de la lumière et de la distance Terre-Vénus exprimée en unités astronomiques permet la détermination de celle-ci en kilomètres. Les ondes radio peuvent pénétrer l'atmosphère terrestre à partir de longueurs d'onde ayant quelques millimètres à près de 100 mètres. Elles induisent alors un léger courant électrique dans un conducteur tel qu'une antenne. Comme les miroirs paraboliques, les antennes paraboliques collectent et rassemblent les ondes radio en leur foyer où un petit courant est créé et amplifié. L'intensité des ondes radio est très faible comparée aux ondes visibles, par conséquent il est nécessaire de disposer de grandes antennes.

Lire la suite ...

Vue d'artiste de Siding Spring dans le ciel de Mars. Crédit : NASA's Goddard Space Flight Center Conceptual Image Lab.

Le 19 octobre dernier, une comète venue des profondeurs du temps et de l'espace a illuminé le ciel de Mars de tout son éclat. Cette comète non périodique est dénommée Siding Spring (C/2013 A1) du nom de l'Observatoire australien où elle a été découverte le 3 janvier 2013 alors qu'elle se trouvait à plus de sept fois la distance de la Terre au Soleil. C'est un coutumier du genre, Robert McNaught qui l'observa le premier grâce au télescope de Schmidt Uppsala de 50 cm. Par la suite, on se rendit compte qu'elle provenait du très lointain nuage de Oort que l'on situe entre 5000 et 100 000 ua et dont les milliards de corps qui le constituent sont des vestiges intacts des premiers âges du système solaire.

Son périple vers l'intérieur du système solaire a dû commencer il y a près d'un million d'années. Il n'est pas anodin de noter que le destin de Mars aurait pu être scellé dès ce moment car, le 19 octobre dernier, Siding Spring a frôlé la planète rouge dont elle n'était distante que de 139 000 km, à peine le tiers de la distance de la Terre à la Lune. La probabilité d'un tel évènement est pratiquement nulle car l'orbite rétrograde et fortement inclinée (129°) ne peut percer le plan de l'écliptique qu'en deux points. Or pour l'un d'eux, Mars s'y trouvait à ce moment précis, un peu comme s'ils s'y étaient donné rendez-vous, à peine six jours avant le passage de la comète à son périhélie situé à une distance de 209 millions de kilomètres du Soleil. Autre coïncidence étonnante, il se trouve que la planète est actuellement celle qui bénéficie des plus grandes attentions des différentes agences spatiales. Ainsi pas moins de cinq sondes orbitent la planète (lancées par la NASA, l'ESA et l'ISRO), dont deux sont arrivées à destination en septembre (MAVEN de la NASA, Mars Atmosphere and Volatile Evolution, et MRO de l'agence spatiale indienne ISRO, Mars Orbiter Mission), et deux rovers se déplacent à sa surface (Curiosity et Opportunity). Point d'impact mais en revanche Mars a pu se frotter au sillage de la comète en y pénétrant quelques heures après. Compte tenu de la vitesse très élevée de la comète, près de 200 000 km/h, les différentes agences ont dû mettre à l'abri leurs satellites du côté de la face opposée au passage de la comète de façon à leur éviter la mitraille perforante des poussières éjectées par celle-ci. Les télescopes au sol et spatiaux tout autant que l'armada des instruments d'exploration de Mars ont été tournés vers ce moment unique.

Les prochaines semaines devraient être riches en images et données sur la comète qui nous console de la déception relative de l'an dernier après la désintégration de la comète ISON, autre représentante du nuage d'Oort. Nous pourrions être envieux de Mars car jamais une comète n'est passée aussi près de la Terre. Si Siding Spring avait croisé dans les mêmes conditions l'orbite terrestre, le spectacle aurait été à couper le souffle ; la comète, aussi éclatante que Vénus - donc visible même en plein jour -, aurait lacéré le ciel par son déplacement prodigieux : l'équivalent de trois diamètres apparents lunaires parcourus en une minute ou le ciel tout entier avalé en moins de deux heures. Elle aurait vraisemblablement engendré également les plus grandes craintes et superstitions, véritable oriflamme d'une nouvelle fin du monde annoncée. Finalement, Siding Spring nous laissera sans doute des images superbes et inédites dans le ciel de Mars avant de s'en retourner vers les profondeurs glacées du système solaire d'où elle nous reviendra dans quelques millions d'années, mais elle doit aussi nous inspirer humilité et vigilance et nous rappeler qu'elle aurait pu aussi être cet « astre effrayant » dont parlait Victor Hugo.

Photo prise le 7 février 2008

Comme chaque année début novembre et début février, il est possible d'observer le lever du Soleil juste sous l'arche de l'Arc de Triomphe. Cette observation se fait depuis l'avenue de la Grande Armée. Le seul lieu propice à cette observation est le terre-plein situé au centre du square de la porte Maillot. Depuis ce lieu, le diamètre apparent du Soleil est lègerement plus petit que le diamètre apparent de l'arche de l'Arc de Triomphe, mais si l'on s'éloigne plus de l'Arc de Triomphe, la ligne de visée dans la direction de l'arche recontre des jeux de signalisations disgracieux.

Dates et instants de prises de vue du Soleil dans l'axe de l'arche de l'Arc de Triomphe depuis le square de la Porte Maillot.

Les instants sont en Temps universel ajouter une heure pour avoir l'heure légale en France métropolitaine.

ATTENTION : même à faible altitude l'observation directe du Soleil peut être dangereuse pour la vue (et pour votre appareil photo). Pour les photos, il y a risque de surexposition, pensez à prendre un filtre si votre appareil photo ne permet pas de faire de très courtes expositions.

Lever du Soleil dans l'axe de l'arche de l'Arc de Triomphe en 2014

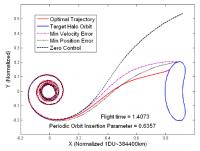
Optimisation d'une trajectoire autour d'un des point de Lagrange. (c) Bruce Conway. Le point de départ de la trajectoire est en (0,0), sur Terre. La trajectoire à atteindre est l'orbite bleue. On trouve successivement: la trajectoire noire (aucune optimisation), les trajectoires bleu et mauve (arrivée en une position acceptable, et à une vitesse adaptée), la trajectoire optimisée (en rouge). Les paramètres du problème sont alors, une fois une date de lancement choisie : le nombre de corrections de trajectoires, leur nombre, leur intensité, ainsi que le temps de vol ente le départ et l'arrivée.

Prenez une équation à une inconnue, on peut en général la résoudre sans difficulté. Prenez un système de deux équations à deux inconnues, si le système est linéaire, on établira l'existence ou non d'une solution unique sans davantage de difficultés. Si le système n'est pas linéaire, c'est à dire s'il comporte des expressions autres que des sommes pondérées des inconnues, les choses sont déjà bien davantage corsées, et il n'est pas toujours possible de conclure. Le problème de la résolution des systèmes d'équations est généralisable à un système de n équations à m inconnues. Si le système est linéaire, avec un nombre d'équations égal au nombre d'inconnues, le système est alors dit de Cramer, et admet dans certains cas une solution unique dont on peut donner une formulation générale. Dans le métier de l'astronome, -- comme dans la plupart des métiers scientifiques -- les systèmes d'équations apparaissent dans les phases de modélisation, quand il s'agit de donner une valeur aux paramètres d'un modèle (qui sont alors les inconnues du système), avec des équations caractérisant ce modèle obtenues à partir des observations. L'astronome dispose dans ce cas de bien davantage d'équations que d'inconnues, et c'est d'ailleurs bien là le but d'une modélisation : rendre compte d'une réalité observée au moyen d'un modèle avec le moins de paramètres possibles. Ainsi, on voudra modéliser un nuage de points (potentiellement très nombreux) disposés dans un plan, et grossièrement alignés "à l'oeil", par une droite, caractérisée par seulement deux paramètres : la pente de la droite et l'ordonnée à l'origine. Avec bien davantage d'équations que d'inconnues, il est ainsi notamment possible de minimiser les effets dus à des erreurs de mesure, et d'établir des statistiques fiables sur la qualité des modèles. Il faut cependant pouvoir résoudre un tel système ...

L'un des premiers scientifiques à avoir été confronté à ce problème a été Carl Friedrich Gauss (1777-1855) au début du dix-neuvième siècle, qui cherchait à prévoir la trajectoire de l'astéroîde Cérès récemment découvert. C'est lui qui a formulé le principe de la méthode des moindres carrés, très largement utilisée de nos jours dans de nombreux contextes, et qui permet de déterminer en plus de la solution elle-même des quantités statistiques caractéristiques de l'ajustement, comme les corrélations entre paramètres. Le calcul était alors purement analytique, à la main, et le nombre d'inconnues restait forcément quelque peu limité. En fait, le premier à avoir publié la méthode des moindres carrés est Adrien-Marie Legendre (1752-1833) dans Nouvelles Méthodes pour la détermination des orbites des comète en 1805. Cependant Gauss est bien celui à l'avoir utilisée en premier pour le calcul de l'orbite de Cérès. Comme souvent quand une idée nouvelle est dans l'air du temps, il se trouve qu'elle est découverte simultanément et indépendamment.

Avec les moyens de calcul actuels, ce sont des systèmes à plusieurs centaines voire milliers de milliers d'inconnues qu'il s'agit quelquefois de résoudre, comme en géophysique ou pour construire les modèles climatiques. En mécanique céleste, comme dans d'ailleurs la plupart des domaines de la physique, les équations ne sont cependant jamais linéaires, et c'est le cas de la traduction analytique des lois de Képler... Le seul moyen d'appliquer malgré tout la méthode des moindres carrés consiste alors à linéariser le système, c'est à dire considérer que chaque équation peut s'écrire, au voisinage d'une certaine valeur, comme celle d'une droite. Pour que l'approche soit valable, il faut alors disposer d'une valeur a priori de la solution qui ne soit pas trop éloignée de la véritable valeur recherchée.

Les problèmes en mécanique céleste moderne n'obéissent plus toujours à ce genre de schémas : dans le cas d'un objet nouvellement découvert par l'observation, astéroïdes, comètes, satellites d'astéroïdes, débris spatiaux, etc., aucune information a priori n'est disponible, et il n'est alors pas possible de linéariser les équations du mouvement en vue d'obtenir les conditions initiales à une certaine date. Avec la puissance des moyens numériques actuels, on pourrait alors penser à tester l'ensemble des configurations possibles, mais cela nécessite évidemment bien trop de temps de calcul, n'est pas acceptable scientifiquement, et n'est de toute évidence pas très efficace.

Un certain nombre de méthodes, inspirées des lois de la nature, ont été mises au point au cours des dernières décennies, et peuvent être appliquées à la résolution de systèmes d'équations nombreuses et non linéaires, et sans nécessiter d'informations sur les valeurs a priori des paramètres. Ce sont les méthode de type Algorithmes Génétiques, Colonies de Fourmis, Evolution Différentielle, etc. qui trouvent les solutions par itérations successives. Des moyens numériques importants sont cependant nécessaires pour mettre en oeuvre ces méthodes, et c'est seulement depuis quelques années qu'il est possible de véritablement les appliquer. Il est même possible d'ajouter des contraintes au système d'équations à résoudre, ainsi que l'avait montré Bruce Conway, invité de l'IMCCE au cours de cet automne 2014, lors d'un des séminaires "Temps-Espace". Dans le cas d'une analyse de mission autour de la Terre, par exemple, l'un des critères à optimiser est la visibilité d'un satellite depuis le sol : les "meilleures" orbites répondant à ce critère sont bien évidemment les orbites de hautes altitudes. Dans le même temps, si l'on veut que le satellite puisse également capter le signal des satellites GNSS (dont les GPS), émis depuis ces satellites dans un cône d'environ 20 degrés d'ouverture, il va falloir alors choisir une orbite suffisamment basse pour que la mission puisse également capter ces signaux une partie du temps maximale. Les deux critères entrent alors en compétition, et les algorithmes de type "évolutif" vont trouver le meilleur compromis entre toutes ces contraintes. Parmi les domaines d'application de ces méthodes, on peut citer : la recherche de trajectoires périodiques autour de la Lune, l'optimisation de trajectoires vers les points de Lagrange, l'optimisation de trajectoires dans le système solaire, pour lesquelles une dépense d'énergie minimale peut être recherchée ou un maximum d'astéroïdes visités, la détermination de probabilités de collisions, ou tout "simplement" la recherche de conditions initiales du mouvement. Notons cependant que dans la plupart des cas, une fois les paramètres du système obtenus par l'une de ces méthodes, la méthode des moindres carrés reste utilisée de manière quasiment systématique, pour justement continuer de disposer des corrélations entre paramètres, ce que les méthodes "modernes" ne permettent pas d'obtenir.

Le patrimoine sort de sa réserve

Frontispice de la Connoissance des Temps pour l'année 1765.

Plus besoin de venir à la bibliothèque pour consulter le Bulletin astronomique, la Connaissance des temps ou le Rapport annuel sur l'état de l'Observatoire : tous ces titres sont désormais accessibles en trois clics sur Gallica (http://gallica.bnf.fr/), la bibliothèque numérique de la Bibliothèque Nationale de France (BnF).

Le partenariat avec la BnF devrait se poursuivre en 2015 et concerner les périodiques édités par les observatoires et les sociétés astronomiques françaises.

Comme beaucoup d'institutions, d'académies ou de sociétés savantes, l'Observatoire a eu une activité éditoriale (http://www.obspm.fr/-edition-et-coeditions-a-l-observatoire-de-paris-.html) importante. C'est aussi le cas du Bureau des longitudes qui a la responsabilité de définir et publier les éphémérides nationales, celles-ci étant réalisées par l'IMCCE (Institut de mécanique céleste et de calcul des éphémérides). Les grandes publications périodiques qu'ils ont éditées comprennent des éphémérides, des données d'observations et des articles scientifiques intéressant tant les astronomes que les historiens de l'astronomie.

Lire la suite ...

Séminaires