À l'intention de nos abonnés

Suite à une évolution de notre organisation informatique interne, nous avons rencontré ce jour des problèmes non anticipés pour l'envoi de la LI d'avril 2015 de l'IMCCE. Nous vous prions de bien vouloir nous en excuser.

Toute coincidence avec la date du jour n'est que fortuite et involontaire.

Éditorial

Avec le numéro 111, la Lettre d'Information de l'IMCCE fête ce mois-ci ses dix ans d'existence, à raison de 11 numéros par an (12 en 2006, avec un numéro spécial consacré à la nouvelle définition des planètes dans le système solaire). Sans relâche, les personnels de l'IMCCE se mobilisent chaque mois (avec un pic d'activité en deuxième quinzaine, reconnaissons-le) pour rassembler les informations astronomiques qu'il nous semble judicieux de porter à la connaissance de l'ensemble de nos abonnés dont vous faites partie, dans un langage censé être le plus accessible possible. Il s'agit d'un exercice particulier pour les chercheurs, qui s'y prêtent toujours bien volontiers (quelquefois après plusieurs relances) pour faire un point en quelques lignes sur les projets de recherche ; il s'agit d'une valorisation des calculs du Service des Ephémérides, pas tous faits de manière automatique ; il s'agit aussi d'une valorisation de l'ensemble des services de l'IMCCE, dont le service des Editions, et c'est au final une vision d'ensemble des activités du laboratoire qui émane de chacune des "L.I.", comme nous l'appelons en interne. Bon an mal an, nous avons toujours réussi à vous envoyer la "L.I." en temps et en heure, même si cela a été "chaud" certains mois.

Notre but de rendre l'astronomie et la mécanique céleste facilement accessibles est-il atteint ? Vous pouvez nous le dire. La réponse peut-être "oui" si vous savez que le Soleil est en Poisson au cours du mois d'avril, et qu'il n'est pas inhabituel de voir une éclipse de Lune arriver un demi-mois après une éclipse de Soleil, ou que vous voyez dans l'orbite du mois présentée dans le feuilleton autre chose que le symbole d'une action caritative bien connue ; la réponse peut être "non" si comme nous, vous vous êtes étonnés de la circulaire de l'Education Nationale prônant un principe de précaution décliné à l'extrême voire même déresponsabilisant, comme le mentionne non sans quelques points d'ironie l'article de notre collègue Hervé Dole paru dans le Monde du 19 mars . Dans tous les cas, ce sont de bonnes raisons de rester abonné et de faire abonner à la L.I. de l'IMCCE.

Nous ne manquons pas d'idées pour la suite, mais nous vous invitons à nous faire des suggestions de thèmes que vous voudriez voir traités au cours des prochaines années, par exemple dans le cadre de nouveaux feuilletons. Chaque numéro est un véritable projet à mener en équipe, et de prochains défis nous attendent à nouveau pour les prochains mois et prochaines années. Le comité de rédaction a été renouvelé plusieurs fois au cours de ces dix ans. Nous saluons ici le travail de tous les membres et tous les rédacteurs, et en particulier les collègues qui ont initié le projet en 2005, ainsi que les personnels techniques qui ont fait évoluer la maquette. Le nombre des abonnés ne cesse de croître, atteignant en 2015 plus de 2300 abonnés avec une adresse E-mail valide.

Le comité de rédaction.

La Lettre d'information de l'IMCCE a maintenant dix ans. C'est l'occasion de revenir sur les articles que nous vous avons proposés : on trouvera ci-dessous un petit rappel des principaux sujets traités avec le numéro de la lettre concernée depuis 2006 jusqu'à décembre 2014.

Outre des articles sur des sujets particuliers à l'occasion d'une actualité ou d'une date particulière, nous vous avons proposé des « feuilletons » sur un thème donné :

• l'année Galilée (en 2009, à l'occasion du tricentenaire de l'observation du ciel à la lunette)
• la saga des satellites galiléens (en 2010 : la progression de notre connaissance de ces corps complexes et passionnants depuis leur découverte par Galilée)
• Vesta une mini-planète de la ceinture principale des astéroïdes (en 2011)
• l'année Neptune (en 2011, à l'occasion du bouclage d'une première révolution complète autour du Soleil par Neptune depuis sa découverte en 1846)
• Douze hommes en lumière (en 2012, un retour sur les astronomes qui ont apprivoisé la lumière qui nous prodique tant d'information sur le cosmos)
• Chronique d'une fin du monde annoncée (en 2012, à l'occasion de la prédiction de la 184ème fin du monde depuis la chute de l'empire romain, sur les risques que prend la Terre dans sa course autour du Soleil)
• un ciel sur mesure (en 2013, sur la mesure et la cartographie du ciel)
• le patrimoine sort de sa réserve (en 2013 pour découvrir le patrimoine historique de l'observatoire de Paris)
• à la recherche de la parallaxe solaire (en 2014, sur le problème de la mesure des distances dans le système solaire).

Pour voir l'index de ces articles cliquez ici

Visibilité des planètes

(Planètes visibles entre les latitudes 60° Nord et 60° Sud et les constellations les plus voisines)

Mercure est visible le soir au crépuscule à partir du 18 avril, date de sa première visibilité du soir à Paris. Au cours du mois, elle se couchera de plus en plus tard. Elle sera alors dans la constellation du Bélier qu'elle quittera le 28 pour entrer dans la constellation du Taureau.

Vénus est visible tout le mois au crépuscule et en première partie de nuit. Au cours du mois, elle se couche de plus en plus tard, se couchant même après minuit en heure légale française. Elle se trouve dans la constellation du Bélier jusqu'au 7 avril, date où elle entre dans la constellation du Taureau.

Mars est visible au crépuscule et en début de nuit, jusqu'au 16 avril, date de son coucher héliaque du soir à Paris. Tout le mois elle se trouve dans la constellation du Bélier.

Jupiter est visible au crépuscule et une grande partie de la nuit, au cours du mois elle se couche de plus en plus tôt. Elle se trouve tout le mois dans la constellation du Cancer.

Saturne est visible en seconde partie de la nuit et à l'aube, puis une grande partie de la nuit et à l'aube. À partir du 14 mars, elle se lève à Paris avant minuit heure légale française. Au cours du mois, elle se lève de plus en plus tôt. Elle se trouve tout le mois dans la constellation du Scorpion.

Aspect des planètes au 16 avril 2015 Mercure, Vénus, Mars, Jupiter, Saturne, Uranus

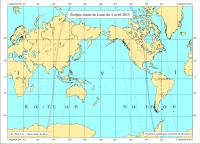
Ciel du mois

Cartes du ciel pour une observation vers le nord et vers le sud
à Paris le 15 avril 2015 à 23 h temps légal

Carte du ciel en direction du nord	Carte du ciel en direction du sud

Ces cartes du ciel montrent les étoiles brillantes et les planètes visibles dans le ciel de l'hémisphère nord, vers l'horizon sud et vers l'horizon nord, pour le 15 avril 2015 (23h). Le trait vertical correspond à la projection sur le ciel du méridien du lieu. L'arc de cercle rouge sur l'horizon sud représente l'écliptique (lieu de la trajectoire apparente du Soleil durant l'année). Les constellations visibles sur ces cartes sont, par ordre alphabétique des sigles :

Andromède (And), la Machine pneumatique (Ant), le Cocher (Aur), le Bouvier (Boo), Cassiopée (Cas), Céphée (Cep), le Grand Chien (CMa), le Petit Chien (CMi), le Cancer (Cnc), la Chevelure de Bérénice (Com), la Couronne Boréale (CrB),le Cratère (Crt), le Corbeau (Crv), les Chiens de Chasse (CVn), le Cygne (Cyg), le Dragon (Dra), les Gémeaux (Gem), Hercule (Her), l'Hydre femelle (Hya), le Lézard (Lac),le Lion (Leo),la Balance (Lib), le Petit Lion (LMi), le Lynx (Lyn), la Lyre (Lyr), la Licorne (Mon), Orion (Ori), Persée (Per), la Boussole (Pyx), la Grande Ourse (UMa), la Petite Ourse (UMi), la Poupe (Pup), le Serpent (Ser), le Sextant (Sex), la Vierge (Vir)

Le Soleil dans sa course apparente sur l'écliptique est accompagné de plusieurs planètes proches. Celles qui sont à l'est peuvent être observées au coucher du Soleil et en début de nuit selon leur élongation et leur magnitude, celles qui sont à l'ouest le seront en fin de nuit et au lever du Soleil sous les mêmes conditions. La figure suivante montre la configuration au 15 avril 2015.

Les cartes du ciel sont générées à l'aide du logiciel libre Stellarium.

Nouvelles astronomiques

Carte de visibilité de l'éclipse

Cette éclipse totale de Lune est la troisième éclipse d'une série de quatre éclipses totales de Lune consécutives qui se sont déroulées en 2014 et 2015. La succession de quatre éclipses totales de Lune est un phénomène assez rare, elle se produit 177 fois sur une période de 6000 ans allant de 3000 av. J.-C. à 3000 apr. J.-C. Cela se produira de nouveau en 2032 et 2033. Il n'existe pas de successions de cinq éclipses totales de Lune consécutives.

Pour voir les différentes phases d'une éclipse de Lune en un lieu donné, il suffit qu'il fasse nuit durant ces phases. En effet, les éclipses de Lune se produisent toujours à la pleine Lune. Or à la pleine Lune, la Lune se lève lorsque le Soleil se couche et elle se couche lorsque le Soleil se lève, la Lune est donc visible toute la nuit. Depuis le sol français et l'Europe aucune des phases ne seront observables. La phase de totalité ne durera que 5min 37s.

La carte (ci-contre) est centrée sur la zone de visibilité (V) et de chaque côté on trouve deux zones d'invisibilités (I), en fonction du type d'éclipse on a tracé plusieurs courbes :

• P1 : la limite de la région où l'on observe l'entrée dans la pénombre (petits pointillés)
• O1 : la limite de la région où l'on observe l'entrée dans l'ombre (grands pointillés)
• T1 : la limite de la région où l'on observe l'entrée dans la totalité (trait plein)
• T2 : la limite de la région où l'on observe la fin de la totalité (trait plein)
• O2 : la limite de la région où l'on observe la sortie de l'ombre (grands pointillés)
• P2 : la limite de la région où l'on observe la sortie de la pénombre (petits pointillés)

Chacune de ces courbes correspond aux lieux où la Lune se trouve à l'horizon à l'instant de la phase correspondante, les courbes en rouge correspondent aux lieux où la Lune se lève et les courbes en bleu les lieux où la Lune se couche. Pour chaque phase, les lieux situés à l'ouest d'une courbe rouge ne voient pas le début de la phase car la Lune n'est pas encore levée et les lieux situés à l'est voient la phase correspondant à la courbe car la Lune est déjà levée. De même, les lieux situés à l'est d'une courbe bleue ne voient pas la phase car la Lune est déjà couchée et les lieux situés à l'ouest voient la phase correspondant à la courbe car la Lune n'est pas encore couchée.

Déplacement de la Lune durant l'éclipse, la figure est centrée sur la
position des cônes d'ombre et de pénombre à l'instant du maximum.

Cette éclipse a lieu deux jours après le passage de la Lune à son apogée, le diamètre apparent de la Lune sera donc faible (29,74'). L'éclipse aura lieu après le passage de la Lune par son noeud ascendant. Voici la suite des événements relatifs à la Lune sur cette courte période de temps :

• le 01/04/2015 à 13h 00m 49s UT : la Lune à l'apogée (distance maximale à la Terre) d = 406011,781 km, diam. app. : 29,51' long. moy. : 159,25°.
• le 03/04/2015 à 01h 40m 13s UT : la Lune a une déclinaison nulle et décroissante, asc. droite = 11h 48,2m.
• le 04/04/2015 à 03h 17m 35s UT : la Lune passe par le nœud ascendant de son orbite, long. moyenne : +190° 0,7'.
• le 04/04/2015 à 12h 05m 34s UT : Pleine Lune.

Des lecteurs nous ont demandé avec quelles fréquences les éclipses de Soleil se reproduisaient le jour de l'équinoxe de printemps.

Ce problème revient à trouver une période de récurrence des éclipses qui ramène les éclipses à une même date du calendrier grégorien.

Les périodes de récurrence des éclipses sont des périodes multiples de la révolution synodique moyenne L de la Lune (qui ramène la même phase lunaire) et de la révolution draconitique moyenne D de la Lune qui ramène la Lune à un de ces nœuds. On peut distinguer deux types de périodes de récurrences, celles sans changement de nœud et celles avec changement de nœud.

Si l'on ne change pas de nœud, on recherche deux entiers p et q tel que : q  L = p  D ce qui revient à trouver une représentation du nombre réel L/D par une fraction p/q de deux entiers.

Si l'on cherche une récurrence avec changement du nœud de l'orbite lunaire alors on doit chercher deux entiers p et q tel que : q x L = p x D/2, p étant un entier impair.

On trouve de nombreuses solutions à ces problèmes, les deux plus connues sont le Saros et l'Inex

La période dite du Saros (S) correspondant à 3858,32 jours (18,03 années juliennes) soit 223 lunaisons et 242 révolutions draconitiques pour une récurrence au même nœud de l'orbite lunaire. Cette période de récurrence est particulièrement stable, car elle est également un multiple de la révolution anomalistique moyenne A qui ramène la Lune à une même position par rapport à la direction de son périgée (239 A). Les séries longues d'éclipses correspondant à cette récurrence comportent entre 65 et 73 éclipses consécutives.

La période dite Inex (I) correspondant à 10571,95 jours (28,94 années juliennes) soit 358 lunaisons et 388,5 révolutions draconitiques (p = 777) pour une récurrence avec changement de nœuds. Les séries longues d'éclipses correspondant à cette récurrence comportent entre 786 et 872 éclipses consécutives.

Avec : L = 29,530 588 853 jours, D = 27,212 220 817 jours et A = 27,554 549 878 jours, on peut démontrer que toutes les périodes de récurrence sont des combinaisons linéaires de ces deux périodes.

Si une éclipse de Soleil a lieu à une date donnée du calendrier, la suivante aura lieu 19 ans plus tard, c'est le cycle de Méton M qui comporte 235 lunaisons. On peut démontrer que : M = 10 I – 15 S. Par contre le nombre d'éclipses se succédant à un cycle de Méton d'intervalle est faible, il ne comporte que 4 ou 5 éclipses consécutives.

On peut également rechercher quel intervalle sépare deux séries d'éclipses séparées par un cycle de Méton. Dans ce cas on doit rechercher trois nombres p, q et r tel que : q x L = p x D = r x G, où G est la durée calendaire moyenne du calendrier grégorien (365,2422 jours). On trouve la solution suivante : q = 4601, p = 4993 et r = 372. Donc tous les 372 ans, on retrouve une éclipse de Soleil un 20 mars. Ces séries espacées de 372 ans comportent également peu d'éclipses (6 à 7 éclipses).

Cette période peut également se mettre sous la forme d'une combinaison linéaire du Saros et de l'Inex : 4601 x L = 11 x S + 6 x I.

En utilisant le canon d'éclipse de Soleil élaboré à l'IMCCE, nous avons trouvé les séries d'éclipses suivantes :

Tableau 1 : éclipses tombant le jour de l'équinoxe depuis le début du calendrier grégorien jusqu'en l'an 3000.
Remarques : pour les éclipses portant sur deux jours consécutifs, les instants du maximum supérieurs à 12h correspondent au premier jour et les instants du maximum inférieurs à 12h correspondent au second jour. Les lignes de même couleur correspondent à des éclipses espacées de 372 ans.

Si l'on utilise le calendrier grégorien proleptique pour les dates antérieures à 1582, on peut remonter plus haut dans le temps et rechercher les éclipses associées à celle de 20 mars 2015 et séparées de 372 ans. On trouve bien une série de sept éclipses remontant à l'an 155.

Remarque : on constate parfois un décalage entre le jour de l'équinoxe de printemps et la date de l'éclipse, cet écart a deux origines : une légère dérive due à la période de 372 ans et le fait que les durées des saisons ne sont pas constantes en raison de l'avance du périhélie de la Terre.

Séminaires

Les Lois de Képler dans tous leurs états

Nous repartons ce mois-ci à des altitudes plus élevées que le mois précédent, en nous intéressant à une classe d'orbite appelée HEO, pour "Highly Elliptical Orbit". Le but pour cette famille d'orbite est d'atteindre des altitudes extrêmement élevées, proches dans certains cas de la distance Terre-Lune, pour répondre à des objectifs scientifiques particuliers. Luna-3, la première mission envoyée par les Soviétiques pour observer la face cachée de la Lune, en 1959, était en fait un satellite de la Terre envoyé sur une telle trajectoire. En orbite quasi-polaire, la période était alors d'une quinzaine de jours, avec un périgée à 480 000 km et un périgée à 40 000 km.

Les deux fiches que nous vous proposons de télécharger décrivent les propriétés des orbites HEO. La première concerne les orbites Molnya, très largement utilisées pour les besoins de communication en Russie, avec une période de 12 heures (demi jour sidéral) ; la deuxième fiche décrit les trajectoires de deux missions scientifiques, XMM-Newton et Integral, qui nécessitent d'avoir des altitudes extrêmement élevées pour s'affranchir des radiations dues à la Terre.

Documents PDF

• Fiche : l'orbite de type HEO des Molnyia

• Fiche : l'orbite de type HEO de XMM-Newton et Integral

	XMM @ESA operation
	Integral

En direct du Laboratoire

Lucie Maquet de l'ESA a développé en mars les thèmes qu'elle développe sur les occultations stellaires, et l'instrument MIOSOTYS.

La population de la ceinture de Kuiper est encore relativement mal connue : étant située loin de la Terre, les corps qui la composent sont difficiles à observer. Un peu plus de 1300 objets majeurs d'un diamètre supérieur à 30 km ont été découverts au-delà de Neptune. Pour pouvoir comprendre comment la ceinture de Kuiper s'est formée, il faut pouvoir étudier la répartition en taille des objets qui la composent. Il faut donc être capable de détecter les objets les plus petits. Cela n'est possible que par occultations stellaires aléatoires. Le principe consiste à observer un champ d'étoiles et détecter un phénomène de diffraction lorsque qu'un petit objet (sub-kilométrique) passe devant une étoile. Pour cela, le LESIA possède un instrument MIOSOTYS (Multi-object Instrument for Occultations in the SOlar system and TransitorY System), photomètre multifibre qui a été installé d'abord sur le télescope de 193cm de l'Observatoire de Haute-Provence et à présent sur le télescope de 123 cm de l'Observatoire de Calar-Alto en Espagne. Cet instrument assure l'observation d'une trentaine d'étoiles par champ avec une fréquence d'acquisition élevée, ce qui permet d'observer le phénomène de diffraction nécessaire pour déterminer la taille et la distance des objets détectés. Grâce à cet instrument, nous avons observé plus de 5000 h étoile permettant d'obtenir plusieurs détections. Lucie Maquet a ainsi débuté une étude statistique sur la répartition des objets sub-kilométriques, étude nécessaire pour comprendre les mécanismes de formation de la ceinture de Kuiper et donc par cascade, pour approfondir notre connaissance de la formation du Système Solaire.

Intégrer numériquement le système solaire pendant des dizaines ou des centaines de millions d'années en identifiant certaines résonances à l'origine des principales instabilités, et voici les mathématiques de Lagrange, Poincaré, Arnold intimement liées au développement de méthodes numériques raffinées telles que l'analyse en fréquence, mais également au développement d'un nouveau logiciel de calcul formel. Se rendre compte ensuite, d'une part de ce que l'exploration globale d'un espace des phases ainsi rendue possible s'exporte aisément vers les accélérateurs de particules, d'autre part de ce que les fréquences mises en évidence sur de très longues périodes dans les approximations quasi-périodiques de la variation des excentricités ou des fréquences séculaires planétaires rejoignent les recherches des géologues sur les paléoclimats et permettent même, par la comparaison aux fréquences trouvées dans les carottes glaciaires, une calibration fine de ceux-ci, et voici que la diversité des origines des intervenants dans ce colloque ne masque plus ce qui les réunit.

International Workshop in Astronomy and Dynamics

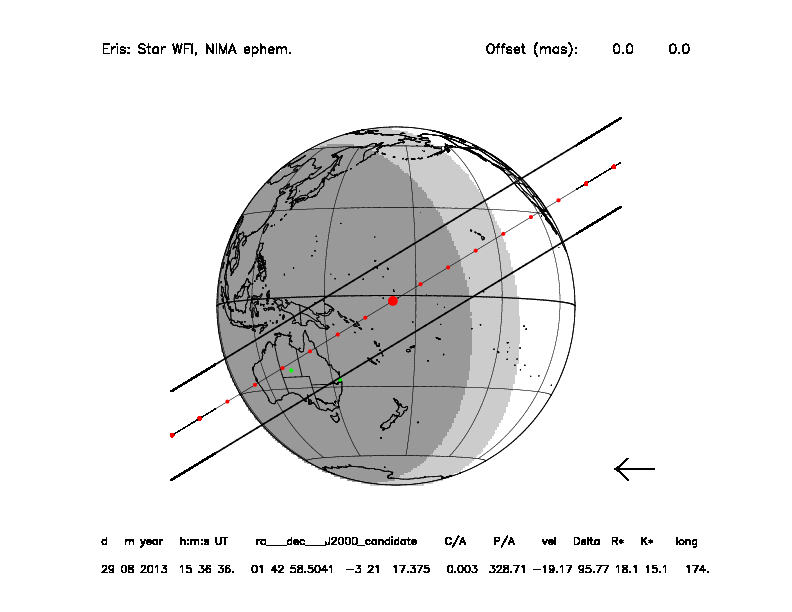
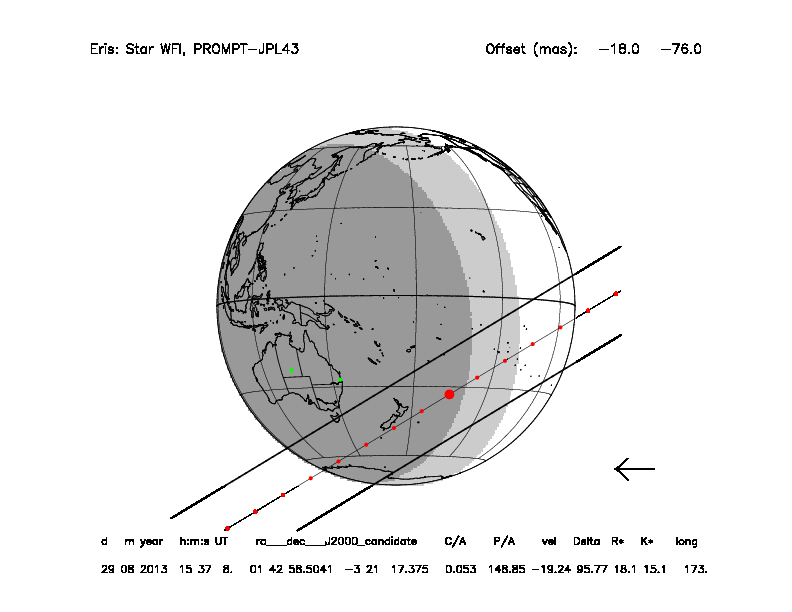
Prédiction d'occultations stellaires par les objets transneptuniens. Josselin Desmars.

Les objets transneptuniens sont des petits corps célestes qui orbitent au delà de Neptune. Ils forment des éléments de la ceinture de Kuiper, ceinture d'astéroïdes vestige de la formation du système solaire. Leur faible taille (quelques centaines de km) et leur éloignement (plus de 30 unités astronomiques) en font des objets difficiles à observer. Une méthode pour étudier ces objets consistent à observer depuis la Terre, leur passage devant une étoile lointaine, ce qu'on appelle une occultation stellaire. Par la mesure de la courbe de lumière de l'étoile pendant cet événement, il est possible de connaître avec précision la taille, la forme de l'objet, de détecter un éventuel satellite, la présence d'une atmosphère ou bien encore un système d'anneau comme par exemple autour de Chariklo.

Pour pouvoir observer ces occultations, il faut savoir où et quand elles seront visibles. Leur prédiction demande de connaître avec précision la position de l'étoile occultée et celle de l'objet occultant. La position de l'étoile est donnée par des catalogues d'étoiles de référence et par l'astrométrie. La position de l'objet est donnée par les éphémérides. Compte tenu de la taille des objets et de leur éloignement, une précision minimale de 50 millièmes de secondes d'arc (50mas) est nécessaire pour la position de l'étoile et la position du corps. Cette taille apparente est équivalent à une pièce de 2€ observée à une centaine de kilomètres de distance, ce qui montre bien la difficulté de la prédiction.

Pour arriver à une telle précision, nous avons développé une méthode de prédiction qui s'appuie sur un modèle dynamique des astéroïdes (NIMA) permettant la détermination d'orbite de l'objet. Ce modèle prend aussi en compte les erreurs systématiques sur les observations qui constituent la principale source d'incertitude de l'orbite. Les observations régulières à la fois de l'étoile (pour une meilleure connaissance de sa position et de son mouvement propre) et de l'objet sont également nécessaires. Ces dernières observations permettent en effet d'affiner l'orbite quelques mois avant l'occultation. Entre mi-2013, date de sa première utilisation, jusqu'à fin 2014, la méthode NIMA a permis, grâce à ses bonnes prédictions, l'observation positive de 15 occultations, soit autant qu'entre 2009 et mi-2013. Elle est désormais utilisée pour les prédictions d'occultations de l'année 2015. Cette méthode permet en particulier des prédictions plus fines et la concentration des moyens d'observations dans les zones concernées afin de multiplier les sites d'observations et par conséquent le nombre de cordes permettant de mesurer le maximum d'informations sur ces objets. La figure montre un exemple de carte de prédiction d'occultation par (136199) Eris le 29 août 2013. La première carte montre que la zone de visibilité de l'occultation prédite par l'ancienne méthode passe sur la Nouvelle-Zélande alors que la seconde, celle prédite par la méthode NIMA, montre que cette zone passe plutôt sur l'Australie. Au final, cette occultation a été détectée dans deux sites australiens (points verts sur la carte) montrant la meilleure prédiction grâce à la méthode NIMA.

A l'avenir, le catalogue d'étoiles de référence Gaia donnera des positions d'étoiles très précises. La position de l'objet sera alors la principale source d'incertitude pour réaliser de bonnes prédictions. Il faudra donc affiner encore les éphémérides de ces objets pour maintenir et perfectionner la qualité des prédictions.

Ce travail est réalisé en collaboration avec l'Observatoire de Rio de Janeiro et le LESIA.