Visibilité des planètes

(Planètes visibles entre les latitudes 60° Nord et 60° Sud et les constellations les plus voisines)

Mercure est visible le soir à l'ouest au coucher du Soleil jusqu'au 13 mars, date de sa dernière visibilité du soir à Paris. Elle est tout le mois dans la constellation des Poissons.

Vénus est visible tout le mois le soir au crépuscule et en première partie de la nuit. Au cours du mois, elle se couchera de plus en plus tard et sera donc visible plus longtemps. À partir du 26 mars elle se couchera après minuit en temps légal français. Elle se trouve dans la constellation des Poissons jusqu'au 4 mars, date où elle entre dans la constellation du Bélier qu'elle quittera le 30 mars pour entrer dans la constellation du Taureau.

Mars est visible toute la nuit. À partir du 29 mars, date de son coucher héliaque du matin à Paris, son coucher devient visible tôt le matin avant le lever du Soleil. Elle se trouve dans la constellation du Lion.

Jupiter est visible tout le mois au crépuscule et en première partie de la nuit. Au cours du mois, elle se couchera de plus en plus tôt. Elle reste tout le mois dans la constellation du Bélier.

Saturne est visible tout le mois une grande partie de la nuit et à l'aube dans la constellation de la Vierge. Au cours du mois, la planète se lèvera de plus en plus tôt.

Aspect des planètes au 16 mars 2012 Mercure, Vénus, Mars, Jupiter, Saturne, Uranus

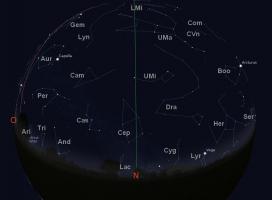
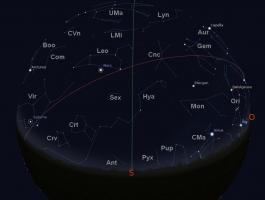
Ciel du mois

Cartes du ciel pour une observation vers le nord et vers le sud
à Paris le 15 mars 2012 à 23 h temps légal

Carte du ciel en direction du nord	Carte du ciel en direction du sud

Ces cartes du ciel montrent les étoiles brillantes et les planètes visibles dans le ciel de l'hémisphère nord, vers l'horizon sud et vers l'horizon nord, pour le 15 mars 2012 (23h). Le trait vertical correspond à la projection sur le ciel du méridien du lieu. L'arc de cercle rouge sur l'horizon sud représente l'écliptique (lieu de la trajectoire apparente du Soleil durant l'année). Les constellations visibles sur ces cartes sont, par ordre alphabétique des sigles :

Andromède (And), le Cocher (Aur), la Machine pneumatique (Ant), le Bélier (Ari), le Bouvier (Boo), la Girafe (Cam), Cassiopée (Cas), Céphée (Cep), le Grand Chien (CMa), le Petit Chien (CMi), le Cancer (Cnc), la Chevelure de Bérénice (Com), la Couronne Boréale (CrB),le Cratère (Crt), le Corbeau (Crv), les Chiens de Chasse (CVn), le Cygne (Cyg), le Dragon (Dra), les Gémeaux (Gem), Hercule (Her), l'Hydre femelle (Hya), le Lézard (Lac),le Lion (Leo), le Lièvre (Lep), le Petit Lion (LMi), le Lynx (Lyn), la Lyre (Lyr), la Licorne (Mon), Orion (Ori), Persée (Per), la Boussole (Pyx), la Grande Ourse (UMa), la Petite Ourse (UMi), la Poupe (Pup), le Sextant (Sex), le Taureau (Tau), le Triangle (Tri), la Vierge (Vir).

Le Soleil dans sa course apparente sur l'écliptique est accompagné de plusieurs planètes proches. Celles qui sont à l'est peuvent être observées au coucher du Soleil et au début de nuit selon leur élongation et leur magnitude, celles qui sont à l'ouest le seront en fin de nuit et au lever du Soleil sous les mêmes conditions. La figure suivante montre la configuration au 15 mars 2012.

Les cartes du ciel sont générées à l'aide du logiciel libre Stellarium.

Nouvelles astronomiques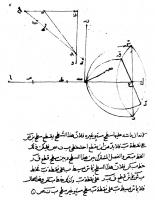

En haut à gauche se trouvent, confondus, deux triangles rectangles figurés par les deux hypoténuses. L'hypoténuse intérieure représente le trajet d'un rayon lumineux tombant sur une surface plane de cristal. L'hypoténuse extérieure indique la direction du rayon réfracté. Le côté droit, commun aux deux triangles, exprime la conservation du rapport des sinus – égal au rapport des longueurs des hypoténuses - à la traversée du milieu cristallin.

Dès l'Antiquité, de nombreuses recherches furent menées sur les formes à donner aux surfaces réfléchissantes et réfractrices, capables de concentrer des rayons incidents en un point unique. On savait focaliser les rayons du Soleil au moyen d'un miroir concave : Archimède n'aurait-il pas ainsi embrasé les vêtements des soldats romains qui assiégeaient Syracuse au III^e siècle avant notre ère. Dioclès (vers -240, -180 av. J.-C.), successeur d'Archimède et contemporain d'Appolonius de Perge - célèbre pour ses travaux sur les sections coniques - fut le premier, dans son traité Sur les miroirs ardents, à faire état de la propriété du paraboloïde de révolution de réfléchir tous les rayons du Soleil en un seul et même point si son axe est dirigé exactement vers le Soleil.

Le problème du miroir ardent semblait donc résolu dès lors que les Grecs connurent les lois de la réflexion. Il en allait différemment pour les surfaces réfractrices, baptisées anaclastiques. Leurs formes ne pouvaient être déterminées géométriquement qu'à la condition de connaitre la façon dont le rayon lumineux se brisait au passage d'un milieu transparent - l'air par exemple - à un autre (le cristal, le verre ou l'eau). Au XVII^e siècle, peu après les premières observations de Galilée (Lettre d'Information n°49, 50, 51 et 52), le problème ne semblait toujours pas résolu pourtant il était devenu nécessaire et urgent de comprendre le fonctionnement des lentilles. Il fallait percer la loi de la réfraction. Tour à tour, de façon indépendante, la fameuse loi, dite des sinus, fut découverte successivement, d'abord par Thomas Harriot (1560-1621) dès 1602, puis Willebrord Snell (1580-1626) en 1621 – qui d'ailleurs ne publièrent rien – et enfin, par René Descartes (1596-1650) qui la publia en 1637 dans sa Dioptrique, où il pensa être le premier à avoir déterminé la forme des anaclastiques (c'est lui qui usa du mot de lentille, en raison de l'analogie de forme avec la graine, pour désigner ces petites perles de cristal aux possibilités optiques étonnantes dès lors qu'on leur donnait la forme d'une conique); Kepler s'était également attaqué aux formes des surfaces réfractantes mais sans succès, malgré une correspondance quelque peu stérile avec Harriot.

Pourtant, cette loi avait déjà été éventée quelque 650 ans auparavant ! C'était à la cour Abbasside de Bagdad, où un savant perse, Ibn Sahl (vers 940-1000), tout à la fois mathématicien et physicien, cherchait lui aussi la forme des anaclastiques. C'est dans l'un de ses traités, le Livre des instruments incendiaires (Kitab al-harrāqāt), publié vers 984, qu'il livre cette fameuse loi de la réfraction sous la forme d'une figure (voir ci-contre). Par son dessin, il indique clairement le passage d'un milieu à l'autre par la constance d'un rapport, que l'on sait maintenant être égal à l'inverse de l'indice de réfraction. Le côté droit, commun aux deux triangles droits (dessin en haut à gauche), traduit la quantité qui est ainsi conservée à la traversée du milieu cristallin. Il montre que les rayons lumineux aboutissant sur la surface d'un corps en cristal (dessin en bas à droite), plan-convexe ou biconvexe, de forme hyperbolique, pénètrent ce corps et le traverse en convergeant vers un même point déterminé, qui est le lieu de l'embrasement. À aucun moment, cependant, Ibn Sahl ne commente l'origine physique de ce rapport, et en particulier son lien avec la nature du corps transparent traversé. Le rapport constant des sinus lui offre deux belles anaclastiques : l'ellipse et l'hyperbole. Armé de cette découverte, Ibn Sahl a réalisé un objectif vieux de plusieurs siècles en calculant la forme géométrique d'une lentille à focalisation parfaite. Il ouvre ainsi un nouveau champ d'étude pour les coniques, celui de leurs propriétés optiques. Le lien ainsi établi entre les coniques et les anaclastiques était si indéfectiblement attaché aux instruments ardents que Kepler baptisera naturellement du nom de foyer ces points de convergence, dont l'un d'eux était maintenant occupé par le Soleil, lorsqu'il découvrit que les planètes avaient des orbites elliptiques.

Le manuscrit d'Ibn Sahl n'a été découvert et reconstitué qu'en 1993 par un historien des sciences, Roshdi Rashed, à partir de fragments dispersés entre différentes bibliothèques, à Téhéran et à Damas. L'œuvre d'Ibn Sahl n'a pas jamais irrigué la science médiévale de l'optique. Elle aurait cependant pu être connue à travers les écrits de l'un de ses successeurs directs les plus célèbres, Ibn al Haytham (965-1039) dont la science optique trouvait sa source auprès de ces géniaux précurseurs que furent al-Kindi (LI n°76) et Ibn Sahl. Pourtant il ne reprit pas les travaux de ce dernier sur la réfraction. Ainsi, il faudra encore plus de six siècles à l'Europe médiévale pour retrouver ce qu'Ibn Sahl avait déjà découvert : la forme des lentilles anaclastiques et la loi de la réfraction, sans doute la toute première loi de la nature mathématisée.

Alignement avec la Terre

Les alignements planétaires ont toujours fasciné une certaine catégorie de la population : celle qui craint les signes du ciel. Le rassemblement des planètes, ces astres brillants et mobiles, devait annoncer quelque chose. Si aujourd'hui, ces alignements ne sont plus censés annoncer des événements particuliers et peuvent même être prévus, certains voient en eux un danger de par la configuration que les planètes prennent à ce moment. Voyons tout d'abord ce que l'on entend par « alignements planétaires ».

Lire la suite

Par définition l'instant de l'équinoxe de printemps dans l'hémisphère nord correspond au moment où la longitude géocentrique apparente du centre du Soleil est égale à zéro degré. À cet instant l'ascension droite et la déclinaison du centre du Soleil ne sont pas nulles car la latitude apparente du centre du Soleil n'est pas nulle, mais toutes ces valeurs sont proches de zéro. La direction du Soleil est alors très proche de celle du point gamma, intersection de l'écliptique et de l'équateur céleste. La définition de cette direction est donc unique sur la sphère céleste. Il ne faut pas confondre la direction de l'équinoxe de printemps qui est unique et le fait que le Soleil passe par cette direction. Ainsi dans l'hémisphère nord le début du printemps correspond au passage du Soleil dans la direction de l'équinoxe de printemps alors que ce même phénomène traduit le début de l'automne dans l'hémisphère sud.

Notre calendrier (le calendrier grégorien) est construit de manière à éviter la dérive des dates saisons en conservant une date quasi fixe pour le début de chaque saison.

La date de l'équinoxe de printemps est, en 2012, le mardi 20 mars à 5h 14m 26,9s UTC, soit le mardi 20 mars à 6h 14m 26,9s heure légale française (UTC + 1h).

À cet instant, la latitude géocentrique du centre du Soleil est de 0,70", son ascension droite est de 23h 59m 59,982s et sa déclinaison est de 0,64". Comme on le constate, ces valeurs sont toutes très proches de zéro. C'est pourquoi on dit souvent que le centre du Soleil est dans la direction du point gamma. Néanmoins pour un calcul à la seconde de temps près, le choix de la définition est importante, en effet la déclinaison du centre du Soleil est nulle à 5h 13m 48,12s UTC et l'ascension droite du centre du Soleil est nulle à 5h 14m 34,21s UTC.

Depuis la création du calendrier grégorien (1582) l'équinoxe de printemps tombe le 19, 20 ou 21 mars. Aux XIX^e et XX^e siècles il est toujours tombé le 20 ou le 21 mars. Dans le passé, il est tombé le 19 mars en 1652, 1656, 1660, 1664, 1668, 1672, 1676, 1680, 1684, 1685, 1688, 1689, 1692, 1693, 1696, 1697, 1780, 1784, 1788, 1792 et 1796. Il tombera de nouveau le 19 mars en 2044. Le jour de l'équinoxe, si on fait abstraction de la réfraction atmosphérique, la durée de la nuit est égale à la durée du jour. C'est également le jour où le Soleil se lève plein est et se couche plein ouest.

Cette année l'équinoxe de printemps ne sera pas accompagné par une grande marée d'équinoxe de forte amplitude, le coefficient de la marée de vive-eau la plus proche du 20 mars ne sera que de 92 (le 23 mars), la marée de vive-eau la plus importante du mois sera celle du 10 mars (coefficient 112). Cela est dû à plusieurs circonstances : L'amplitude de la marée est plus forte lorsque les astres sont dans le plan équatorial et lorsque la distance de l'astre à la Terre est minimale (la force de marée est en 1/r³). La grande marée associée à la Pleine Lune du 8 mars sera une marée proche du périgée lunaire et la Lune sera proche du plan équatorial terrestre alors que la grande marée liée à la nouvelle Lune du 22 mars sera une marée proche de l'apogée lunaire.

Voici la succession des phénomènes :

• le 08/03/2012 à 09h 39m 29s UTC : Pleine Lune.
• le 08/03/2012 à 10h 06m 32s UTC : la Lune a une déclinaison nulle et décroissante, asc. droite = 11h 10,0m.
• le 10/03/2012 à 10h 00m 22s UTC : la Lune au périgée (distance minimale à la Terre) d = 362400.341 km.
• le 13/03/2012 à 20h 40m 47s UTC : la Lune passe par le nœud ascendant de son orbite, long. moyenne : +248° 9,5'.
• le 21/03/2012 à 11h 30m 23s UTC : la Lune a une déclinaison nulle et croissante, asc. droite = 23h 9,9m.
• le 22/03/2012 à 14h 37m 07s UTC : Nouvelle Lune.
• le 26/03/2012 à 06h 02m 52s UTC : la Lune à l'apogée (distance maximale à la Terre) d = 405776.505 km, diam. app. : 29.5289' long. : 45.758943'.

Les dates des équinoxes de printemps entre 1583 et 2999

Décalage horaire en Europe

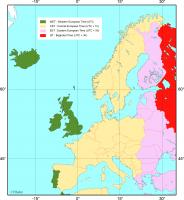
Conformément à l'arrêté du 3 avril 2001 du Ministère de l'économie, des Finances et de l'Industrie, relatif à l'heure légale française, la période d'heure d'été pour l'année 2012 commence le dernier dimanche de mars à 2 heures du matin. Donc, la nuit du 24 au 25 mars 2012, à 2 heures du matin il faut régler les horloges sur 3 heures.

L'horloge parlante, située à l'Observatoire de Paris, diffuse l'heure légale française construite par le Laboratoire National de Métrologie LNE-SYRTE. Elle répond au numéro de téléphone : 36 99. Le début du quatrième top est exact au vingtième de seconde sur tout le territoire métropolitain.

Le choix du méridien de Greenwich comme méridien origine et le découpage de la surface terrestre en 24 fuseaux horaires de 15° datent de la conférence internationale de Washington de 1884. Le temps moyen du méridien origine, le Greenwich Mean Time (GMT) sera remplacé en 1976 par une nouvelle dénomination le Temps universel UT, suivi de différentes variantes, actuellement on utilise le Temps universel coordonné (UTC) lié au Temps atomique international (TAI). L'usage de fuseaux horaires a permis de définir des zones horaires dans lesquelles le écalage horaire avec le Temps universel coordonné est constant. L'Europe est couverte par trois zones horaires définies par un décalage constant avec UTC.

Chaque pays européen a choisi, en fonction de sa longitude, une zone horaire. Chaque pays utilise en plus une heure d'été, cela se traduit, en période d'été, par un décalage horaire d'une heure supplémentaire par rapport à la zone horaire choisie. Afin de faciliter les relations entre pays, les pays de l'Union européenne effectuent leurs passages aux heures d'été et d'hiver, le même jour et au même instant. Un grand nombre des pays européens, non membre de l'Union européenne, font de même, seuls l'Islande, la Biélorussie, la Norvège pour les régions dénommées Svalbard & Jan Mayen ne suivent pas cette règle. En période d'été, les acronymes des noms civils deviennent respectivement WEST, CEST et EEST, la lettre S étant l'initial de « Summer ».

	Communication 2011/C 83/06 de la Commission au sens de l'article 4 de la directive 2000/84/CE du Parlement européen et du Conseil du 19 janvier 2001 concernant les dispositions relatives à l'heure d'été
	Arrêté du 3 avril 2001 relatif à l'heure légale française
	La page du Syrte

Séminaires