Visibilité des planètes

(Planètes visibles entre les latitudes 60° Nord et 60° Sud et les constellations les plus voisines)

Mercure est visible le matin dans les lueurs de l'aube jusqu'au 23 décembre. En début de mois la planète est dans la constellation de la Balance jusqu'au 12, date où elle entre dans la constellation du Scorpion. Puis elle entrera dans la constellation d'Ophiuchus le 16 décembre qu'elle quittera le 29 décembre pour entrer dans la constellation du Sagittaire.

Vénus est visible à l'est en fin de nuit et à l'aube avant le lever du Soleil. Au cours du mois, elle se lèvera de plus en plus tard. Elle se trouve dans la constellation de la Balance jusqu'au 18, date où elle entre dans la constellation du Scorpion qu'elle quittera le 22 pour entrer dans la constellation d'Ophiuchus.

Mars est visible à l'ouest au crépuscule et en début de nuit. Au cours du mois, la planète se couchera de plus en plus tôt. Elle se trouve dans la constellation du Sagittaire jusqu'au 25 décembre, date où elle entrera dans la constellation du Capricorne.

Jupiter est visible toute la nuit et à l'aube, au cours du mois elle se lève de plus en plus tôt. À partir du 11 décembre, date de son coucher héliaque du matin à Paris, elle se couchera avant l'aube. Elle est tout le mois dans la constellation du Taureau.

Saturne est visible en fin de nuit et à l'aube. Au cours du mois elle se lèvera de plus en plus tôt. Elle est se trouve dans la constellation de la Vierge jusqu'au 6 décembre date où elle entrera dans la constellation de la Balance.

Aspect des planètes au 16 décembre 2012 Mercure, Vénus, Mars, Jupiter, Saturne, Uranus

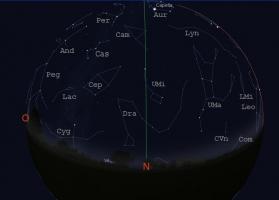
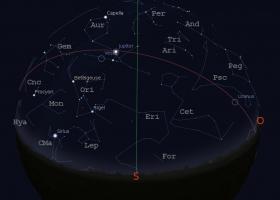
Ciel du mois

Cartes du ciel pour une observation vers le nord et vers le sud
à Paris le 15 décembre 2012 à 23 h temps légal

Carte du ciel en direction du nord	Carte du ciel en direction du sud

Ces cartes du ciel montrent les étoiles brillantes et les planètes visibles dans le ciel de l'hémisphère nord, vers l'horizon sud et vers l'horizon nord, pour le 15 décembre 2012 (23h). Le trait vertical correspond à la projection sur le ciel du méridien du lieu. L'arc de cercle rouge sur l'horizon sud représente l'écliptique (lieu de la trajectoire apparente du Soleil durant l'année). Les constellations visibles sur ces cartes sont, par ordre alphabétique des sigles :

Andromède (And), le Verseau (Aqr), le Bélier (Ari), le Cocher (Aur), la Girafe (Cam), Cassiopée (Cas), Céphée (Cep), la Baleine (Cet), le Grand Chien (CMa), le Petit Chien (CMi), les Chiens de chasse (CVn), le Cygne (Cyg), le Dragon (Dra), Eridan (Eri), le Fourneau (For), les Gémeaux (Gem), le Lézard (Lac), le Lièvre (Lep), le Lion (Leo), le Petit Lion (LMi), le Lynx (Lyn), la Licorne (Mon), Orion (Ori), Pégase (Peg), Persée (Per), le Poisson (Psc), le Taureau (Tau), la Grande Ourse (UMa), la Petite Ourse (UMi), le Triangle (Tri).

Le Soleil dans sa course apparente sur l'écliptique est accompagné de plusieurs planètes proches. Celles qui sont à l'est peuvent être observées au coucher du Soleil et au début de nuit selon leur élongation et leur magnitude, celles qui sont à l'ouest le seront en fin de nuit et au lever du Soleil sous les mêmes conditions. La figure suivante montre la configuration au 15 décembre 2012.

Les cartes du ciel sont générées à l'aide du logiciel libre Stellarium.

Nouvelles astronomiques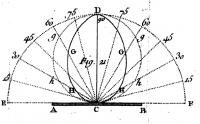

La numératrice des aspérités de Bouguer. Les rayons vecteurs issus de C qui coupent l'une de ces courbes donnent l'intensité de la lumière réfléchie dans une direction donnée. Les angles d'incidence sont comptés à partir de la surface. La courbe en forme de cercle n'est autre que celle d'une surface matte dite Lambertienne. Celle en forme d'œuf résulte de ses expérimentations sur une platine d'argent mais d'une manière plus générale « cette courbe a presque toujours la forme d'une espèce d'ovale moins large que haute, et dont la partie inférieure se termine ordinairement en pointe » (Bouguer, Traité sur la gradation de la lumière, 1760).

Le XVIIIe siècle va voir la naissance d'une nouvelle discipline liée à la lumière, celle de la photométrie. Les artisans principaux en sont Pierre Bouguer (1698-1758) et Johann-Heinrich Lambert (1728-1777). Pour paraphraser Lambert, la photométrie – terme dont il est par ailleurs l'inventeur - « s'occupe de l'éclat de la lumière, de sa densité, de sa force illuminante, […], des accroissements et diminutions qu'elle souffre dans tous les cas ». Il s'agit donc de mesurer l'éclat de la lumière ou sa gradation.

Pierre Bouguer, le premier, donne le ton dès 1729 dans son premier ouvrage Essai sur la gradation de la lumière. Un second ouvrage s'intitulant Traité d'optique sur la gradation de la lumière, plus complet et surtout doté de nombreuses figures, paraîtra de façon posthume en 1760 par les soins de l'Abbé de la Caille. La publication de ce traité est d'ailleurs concomitante à celle de celui de Lambert, Photométrie ou de la mesure et de la gradation de la lumière, des couleurs et de l'ombre (1760), ouvrage entièrement rédigé en latin.

Dans son Essai, Bouguer va jeter les fondements de la photométrie visuelle qui repose sur la propriété de l'œil de pouvoir remarquer avec une excellente précision l'égalité d'aspect de deux surfaces éclairées, lorsqu'elles sont observées en même temps. En effet, l'œil ne peut pas apprécier le rapport de deux intensités lumineuses. Il faut faire en sorte que les sensations provoquées par la lumière provenant de deux sources différentes paraissent identiques en modifiant l'une des deux sources. Comme on aura noté de combien cette dernière aura été modifiée, on pourra connaître le rapport de deux intensités lumineuses. Il utilise la règle selon laquelle « la force de la lumière » est comme l'inverse du carré de la distance de la source à l'écran. C'est armé de ces principes que Lambert entreprendra ses travaux sur la force de la lumière trente ans plus tard, en 1758.

Bouguer va réaliser un grand nombre d'expériences et d'observations. Il détermine ainsi que la lumière du Soleil est environ 300 000 fois plus forte que celle de la pleine Lune ; il va montrer le premier que le disque solaire présente un assombrissement du centre vers le bord ; il va déterminer sous la forme d'une table la variation de l'éclat d'un astre en fonction de sa hauteur et donc de la masse d'air à traverser, car « cette différence de force ne vient que de ce que la lumière a beaucoup moins de trajet à faire dans l'atmosphère, lorsque l'astre est fort élevé, que lorsqu'il est proche de l'horizon » ; il va introduire une courbe, caractéristique des propriétés de réflexion de la surface considérée, qu'il baptise numératrice des aspérités et que l'on appelle de nos jours indicatrice de diffusion. Cette courbe donne la variation de l'intensité de la lumière réfléchie selon la direction d'observation (voir figure). Il y mentionne alors le cas particulier de surfaces dont l'indicatrice se réduirait à un cercle parfait (courbe en pointillés). Ces surfaces sont de nos jours appelées Lambertiennes. Ce sont des surfaces mates de sorte qu'elles paraissent toujours avoir le même éclat quel que soit l'angle sous lequel on les regarde.

Lambert, davantage mathématicien qu'expérimentateur, va d'emblée adopter l'hypothèse simplificatrice de ces surfaces à luminance isotrope (ou mates) lui permettant de mathématiser à l'extrême la photométrie. Dans son ouvrage Photometria il se montre plus méthodique et rigoureux que ne l'est Bouguer. Avec beaucoup de clarté et d'esprit synthétique, il donne véritablement toutes ses lettres de noblesse à la photométrie géométrique. Il énonce des axiomes, démontre des théorèmes dont bon nombre deviendront des lois auxquelles son nom restera attaché comme les fameuses surfaces Lambertiennes précédemment évoquées. Seulement, les objets du réel s'en écartent d'autant plus qu'ils présentent des aspérités et cette déviation augmente avec l'angle d'incidence. C'est tout le problème de la réflexion diffuse de la lumière par des surfaces accidentées auquel s'était attaqué Bouguer et que Lambert laissa de côté. L'entreprise était bien hardie car elle ne trouva qu'un début de réponse que dans les années 1930 avec Opik (1924) et Minnaert (1941) notamment afin de mieux expliquer la réflexion lunaire, corps typiquement non-Lambertien comme l'avait déjà souligné Bouguer. Depuis une vingtaine d'années, les recherches ont repris de plus belle en raison des applications liées à la vision par ordinateur, par exemple dans les méthodes SFS (Shape From Shading) où il s'agit de reconstruire la forme 3D d'un objet à partir de la perception fournie par une image ombrée à deux dimensions.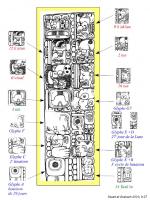

Inscription arrière, Stèle 3 (partie supérieure), Piedras Negras, Guatemala. Dessin: Davis Stuart [Stuart et Graham 2003:9:27].

Les Mayas, parallèlement à leur calendrier rituel qui a le défaut de se reproduire à l'identique tous les 52 ans, utilisaient un calendrier, nommé le long compte, basé sur le décompte des jours depuis une date origine. Ce calendrier ressemble à la période julienne introduite par J. J. Scaliger (1540-1609) en 1583. L'unité de base du long compte est le tun d'une durée de 360 jours. Un tun se décompose en 18 winal (mois de 20 jours), le jour étant un kin. Les multiples du tun (en base vigésimale) sont respectivement : le k'atun (20 tun), le b'ak'tun (20 k'atun), puis le pik'tun (20 b'ak'un), le kalab'tun (20 pik'tun), le k'inchil'tun (20 kalab'tun) et le Alau'tun (20 k'inchil'tun).

Le problème de la concordance entre notre calendrier et les calendriers mayas est connu sous le nom de corrélation. Cette concordance se fait par l'intermédiaire du jour julien de la période julienne. Cette corrélation est la valeur de la différence entre l'origine du long compte maya et l'origine de la période julienne. Si l'on connaît la valeur de cette corrélation, il suffit d'y ajouter le long compte pour avoir le jour julien, puis de transcrire ce jour julien dans le calendrier de notre choix (calendrier julien ou calendrier grégorien).
Depuis le début du xxe siècle, de nombreux chercheurs (historiens ou astronomes) se sont penchés sur ce problème et le grand nombre de solutions proposées (plus de 50) et leurs fortes amplitudes (1039 ans d'écart entre les deux corrélations extrêmes) sont des indicateurs de la difficulté du problème. Les premières recherches furent entreprises par des historiens. Elles sont basées sur les concordances entre des dates du calendrier julien et du calendrier rituel encore en usage à l'époque de la conquête espagnole. Après de nombreuses divergences, les historiens, depuis le milieu du xxe siècle, privilégient la corrélation 584283 dite GMT (pour Goodman - Martínez - Thompson). Si cette corrélation explique bien les dates du calendrier rituel de l'époque postclassique, elle présente des problèmes avec les dates des tables astronomiques présentes dans le codex de Dresde. Des astronomes ont également proposé des solutions basées sur l'interprétation les tables du codex et des dates des saisons gravées sur les stèles (Copán, Piedras Negras et Quiriguá). Mais de nouveau, plusieurs solutions ont vu le jour en fonction des hypothèses de calcul. Le problème d'interprétation des dates du codex est complexe. En 1996, V. Böhm et B. Böhm, en partant de l'hypothèse que les premières dates figurant dans les tables étaient des dates d'observations et en utilisant une méthode statistique ont abouti à quatre valeurs possibles pour la corrélation (438906, 530584, 600070 et 622261). Parmi ces quatre valeurs, seule la dernière, la corrélation 622261, permet de retrouver les maximums d'élongation de Mercure. Douze ans plus tard, la même étude a été refaite en utilisant une méthode statistique plus stricte et de nouvelles dates portant sur d'autres phénomènes astronomiques (conjonctions planétaires). La corrélation 622261 a été confirmée et des explications convaincantes, basées sur le saut de 17 jours dans les porteurs de l'année, ont été émises pour expliquer les concordances de l'époque de Diego de Landa. Néanmoins, cette nouvelle corrélation n'a pas pour l'instant convaincu les historiens, et ils continuent d'utiliser la corrélation GMT qui s'est imposée au fil des années.

Platon dans le Timée (39 C-D) définit l'année parfaite comme la période à la fin de laquelle les planètes se retrouvent toutes alignées sur leurs orbites. Aristote la nomme la grande année et précise que dans l'hiver de cette année il y aura des cataclysmes et que durant l'été il y aura une conflagration. Cette idée d'un univers cataclysmique et cyclique, qui débute avec un alignement parfait des astres errants et se termine lorsque l'alignement se reproduit, se retrouve dans de nombreuses civilisations. Si Platon et Aristote n'indiquent aucune durée pour cette période, Censorinus nous donne des valeurs très différentes : 2484 ans (Aristarque), 10800 ans (Héraclite), 10884 ans (Dion), 120000 ans (Orphée) et 3600000 ans (Cassandre). On dispose d'une valeur introduite en Grèce en même temps que l'astrologie par le prêtre chaldéen Bérose qui estime cette période à 120 saros de 3600 ans (soit 432000 ans). On retrouve les mêmes doctrines dans les textes indiens du Mahâbhârata et des Lois de Manu du IIe siécle. Aux Indes, cette période intervient également dans la description des yugas et des âges du monde : ainsi le Kaliyuga est une période de 1200 années des dieux de 360 ans. Ces cycles n'ont aucune réalité physique, la connaissance des révolutions sidérales moyennes des planètes, même arrondies aux jours, donne une hypothétique période synodique des planètes plus grande que l'âge actuel de l'Univers !
De même, les Mayas ont une vision cyclique du temps associée à la période de 13 b'ak'tun et comme d'autres civilisations ils associent la fin de ces cycles à des destructions et le début des nouveaux cycles à un renouveau. On trouve peu de traces de ces croyances, uniquement dans les Chilam Balam et dans un texte sur le monument n°6 du site de Tortuguero1. Ces dernières décennies, on a vu apparaître une multitude de prédictions apocalyptiques irréalistes liées à l'hypothétique fin du présent cycle le 21 décembre 2012 (avec la corrélation GMT). Sans aucun discernement ni aucune vérification, de nombreux médias, en quête de sensationnel, ont amplifié cette désinformation. D'un point de vue astronomique le 21 décembre 2012 sera un jour particulièrement « calme » : aucun alignement de planètes, pas même une petite conjonction. Comme chaque année, nous serons proches du solstice d'hiver et le Soleil croisera le plan galactique. Il y a de fortes chances que l'absence de catastrophes planétaires ce jour sera associée à une erreur de corrélation plutôt qu'à une remise en cause des prophéties cataclysmiques.

Les calendriers Maya

Cette année, le solstice d'hiver tombe le vendredi 21 décembre à 11h 11m 37,74s UTC, c'est-à-dire le vendredi 21 décembre à 12h 11m 37,74s en heure légale française.
Cette date marque le début de la saison. C'est la date où, sous nos latitudes, le Soleil se lève le plus au sud-est (son amplitude ortive est maximum) et se couche le plus au sud-ouest (son amplitude occase est maximum). C'est également la date où la durée de la nuit est maximale et la durée du jour est minimale. À partir du solstice d'hiver les jours recommencent à croître, mais pas de manière symétrique le matin et le soir. En effet nous utilisons comme échelle de temps un Soleil moyen, ainsi le Soleil continue de se lever en temps moyen de plus en plus tard même après le solstice (jusqu'au 2 janvier), alors qu'en début de mois de décembre, l'heure du coucher du Soleil décroît jusqu'au 13 décembre puis se met à croître.

Le terme solstice vient du latin solstitium (de sol « soleil » et sistere « s'arrêter, retenir ») car l'azimut du Soleil à son lever et à son coucher semble rester stationnaire pendant quelques jours à ces périodes de l'année, avant de se rapprocher à nouveau de l'est au lever et de l'ouest au coucher. À l'instant du solstice d'hiver, le Soleil entre dans le signe du Capricorne mais pas dans la constellation éponyme ; l'entrée dans le signe du Capricorne correspond à une longitude apparente du Soleil de 270° et à ce moment là, le Soleil est dans la constellation du Sagittaire. Ce jour là il passe au zénith pour un observateur de l'hémisphère sud situé sur le tropique; ce qui explique l'origine de son nom : le tropique du Capricorne.
Attention l'instant du solstice d'hiver correspond à l'instant où la longitude apparente du Soleil est égale à 270° et non à l'instant où la déclinaison du Soleil est minimale (23h 45m 46,0s UTC).

Notre calendrier, le calendrier grégorien, est un calendrier solaire. Il a pour but d'éviter la dérive des dates des saisons. La durée des saisons variant sur de grandes périodes de temps, il est impossible de maintenir fixes les dates des saisons, tout au plus est-on capable d'éviter leurs dérives.

Dans le calendrier grégorien le solstice d'hiver peut tomber le 20, 21,22 ou 23 décembre. Il tombe en général le 21 ou le 22 décembre. Il est tombé un 23 décembre en 1903 et tombera de nouveau à cette date en 2303, 2307, 2311 et 2315. Il est tombé un 20 décembre en 1664, 1668, 1672, 1676, 1680, 1684, 1688, 1692, 1696 et 1697 et tombera de nouveau à cette date en 2080, 2084, 2088, 2092, 2096, 2488, 2492 et 2496.

	La Sainte Luce
	Les solstices d'hivers entre 1583 et 2999
	L'évolution des dates des saisons

Image, réalisée par l'instrument SOFI sur le télescope NTT de l'ESO à l'Observatoire de La Silla, montrant la planète errante CFBDSIR J214947.2-040308.9 dans l'infrarouge. Crédit: ESO/P. Delorme

Dans l'Antiquité, les grecs eurent la bonne idée de baptiser tout ce qui n'était pas fixe dans le ciel du nom d'astres errants, ce qui donna naissance au mot planète. Cependant, les planètes ainsi comprises font références à ces corps froids voués à tourner, en solitaire ou en groupe, autour d'une étoile centrale. Il vient pourtant d'être découvert, non loin de notre système solaire, un objet atypique, rouge sombre, froid (430°C), de faible gravité et de faible masse, que l'on oserait dénommé planète errante s'il n'y avait cette redondance étymologique.

Cet objet, au nom barbare et absolument imprononçable de CFBDSIR J214947.2-040308.9 dont nous sommes distants d'à peine 100 années-lumière, situé dans la constellation du verseau, est l'un des tous premiers membres d'une nouvelle catégorie du bestiaire astronomique, celle des IPMO (Isolated Planetary Mass Object) ou encore OIMP en français (Objet Isolé de Masse Planétaire). Plus simplement, c'est une planète flottante ayant une masse comprise entre 4 et 7 fois la masse de Jupiter, n'appartenant à aucun système stellaire si ce n'est un courant d'étoiles jeunes, AB Doradus, âgé de 50 à 120 millions d'années. Son origine est encore incertaine ; elle peut être issue de la fragmentation d'un nuage interstellaire qui a donné naissance à ce courant d'étoiles ou avoir été éjectée d'un système stellaire dont elle était l'un des membres. On savait déjà que les étoiles de très faibles masses, les naines brunes, formaient la composante stellaire dominante de notre galaxie (75% des étoiles) mais ce nouveau type d'objets, encore plus froid et plus sombre, existe probablement en très grand nombre également.

Perdue dans l'espace : une planète solitaire repérée

Séminaires