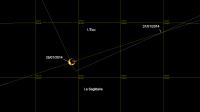
Visibilité des planètes

(Planètes visibles entre les latitudes 60° Nord et 60° Sud et les constellations les plus voisines)

Mercure est visible le soir à partir du 17 janvier, date de sa première visibilité du soir à Paris, elle sera alors dans la constellation du Capricorne, qu’elle quittera le 29 pour entrer dans la constellation du Verseau. Elle atteindra sa plus grande élongation est le 31 janvier.

Vénus est visible le soir jusqu’au 9 janvier puis elle redeviendra visible le matin à partir du 12 janvier, date de sa première visibilité du matin à Paris. En début de mois, elle se trouve dans la constellation du Sagittaire, jusqu’au 25 date où elle entrera dans la constellation du Bouclier qu’elle quittera le 31 pour revenir dans la constellation du Sagittaire.

Mars est visible tout le mois la seconde partie de la nuit et à l’aube dans la constellation de la Vierge.

Jupiter est visible une grande partie de la nuit et à l’aube dans la constellation des Gémeaux. À partir du 18 janvier, date de son coucher héliaque du matin à Paris, elle se couchera avant l’aube.

Saturne est visible en fin de nuit et à l’aube dans la constellation de la Balance. Au cours du mois, elle se lèvera de plus en plus tôt.

Aspect des planètes au 16 janvier 2014 Mercure, Vénus, Mars, Jupiter, Saturne, Uranus

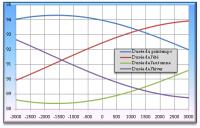
Ciel du mois

Cartes du ciel pour une observation vers le nord et vers le sud
à Paris le 15 janvier 2014 à 23 h temps légal

Carte du ciel en direction du nord	Carte du ciel en direction du sud

Ces cartes du ciel montrent les étoiles brillantes et les planètes visibles dans le ciel de l'hémisphère nord, vers l'horizon sud et vers l'horizon nord, pour le 15 janvier 2014 (23h). Le trait vertical correspond à la projection sur le ciel du méridien du lieu. L'arc de cercle rouge sur l'horizon sud représente l'écliptique (lieu de la trajectoire apparente du Soleil durant l'année). Les constellations visibles sur ces cartes sont, par ordre alphabétique des sigles :

Andromède (And), le Bélier (Ari), le Bouvier (Boo),le Cocher (Aur), la Girafe (Cam), Cassiopée (Cas), Céphée (Cep),la Baleine (Cet), le Grand Chien (CMa), le Petit Chien (CMi), le Cancer (Cnc), les Chiens de Chasse (CVn), le Cygne (Cyg), le Dragon (Dra), Eridan (Eri), les Gémeaux (Gem), l'Hydre femelle (Hya), le Lézard (Lac),le Lion (Leo),le Lièvre (Lep), le Lynx (Lyn), la Licorne (Mon), Orion (Ori), Pégase (Peg), Persée (Per), la Grande Ourse (UMa), la Petite Ourse (UMi), les Poissons (Psc), la Poupe (Pup), le Taureau (Tau), le Triangle (Tri).

Le Soleil dans sa course apparente sur l'écliptique est accompagné de plusieurs planètes proches. Celles qui sont à l'est peuvent être observées au coucher du Soleil et au début de nuit selon leur élongation et leur magnitude, celles qui sont à l'ouest le seront en fin de nuit et au lever du Soleil sous les mêmes conditions. La figure suivante montre la configuration au 15 janvier 2014.

Les cartes du ciel sont générées à l'aide du logiciel libre Stellarium.

Phénomènes astronomiques

Durées des saisons en jour entre -3000 et +3000.

En 2014 la Terre passera au périhélie le 4 janvier à 11h 58m 34s UTC (12h 58m 34s en temps légal français). La distance du centre de la Terre au centre du Soleil sera alors de 147 104 780,071 km et le diamètre apparent géocentrique du Soleil sera de 32' 31,79". Suite à la seconde loi de Kepler (loi des aires) lorsque la Terre passe au périhélie sa vitesse angulaire est maximale. La vitesse angulaire étant plus rapide au voisinage du périhélie, l'hiver est la saison la plus courte dans l'hémisphère nord.

Voici les dates et les durées des saisons de l'hémisphère nord pour l'année 2014 :

• le 20/03/2014 à 16h 57m 07s UTC : équinoxe de printemps, durée de l'hiver : 88 jours 23h 46m 5,34s.
• le 21/06/2014 à 10h 51m 16s UTC : solstice d'été, durée du printemps : 92 jours 17h 54m 8,75s.
• le 23/09/2014 à 02h 29m 06s UTC : équinoxe d'automne, durée de l'été : 93 jours 15h 37m 50,63s.
• le 21/12/2014 à 23h 03m 03s UTC : solstice d'hiver, durée de l'automne : 89 jours 20h 33m 56,63s.

Sous l'effet des perturbations planétaires, le périhélie avance dans le sens direct d'environ 11,61235" par année julienne. L'axe des apsides fait donc un tour en environ 111915 années juliennes. Comme la droite des équinoxes tourne d'environ 50,38792" par an dans le sens rétrograde, les deux axes sont confondus tous les 20903 années juliennes, cette période porte le nom de précession climatique. En effet, tous les 10451,5 ans (demi-période de la précession climatique) l'aphélie passe du solstice d'été au solstice d'hiver. Or même si la distance Terre-Soleil n'est pas le facteur prédominant dans la nature des saisons, la combinaison du passage de la Terre à l'aphélie en hiver donne des hivers plus rudes. Actuellement la direction du périhélie se rapproche de l'équinoxe de printemps qu'elle atteindra le 24 juin 6430. À partir de cette année l'hiver ne sera plus la saison la plus courte dans l'hémisphère nord mais ce sera progressivement le printemps.

Vénus dans l’Écu du 25 janvier au 31 janvier 2014

Les limites des 88 constellations stellaires ont été définies et publiées par E. Delporte en 1930 sous l’égide de l’Union astronomique internationale (UAI). Les bords de ces limites sont construits sur la sphère céleste, parallèlement à l’équateur céleste ou parallèlement aux cercles horaires.

L’écliptique et le zodiaque rencontrent treize constellations qualifiées de zodiacales. En raison de l’obliquité de l’orbite terrestre et de l’inclinaison orbitale des astres, les planètes et la Lune ne restent pas dans la bande zodiacale. Elles font des incursions dans certaines constellations limitrophes. Vénus, en raison de l’inclinaison de son orbite sur l’écliptique et de son rapprochement avec la Terre est la planète la plus vagabonde. Elle est susceptible de passer dans douze constellations extrazodiacales : l’Aigle, le Cocher, la Baleine, le Petit Chien, la Coupe, le Corbeau, l’Hydre femelle, Orion, Pégase, l’Écu, le Serpent et le Sextant.

Récemment, en 2007, Vénus a fait un passage dans la constellation du Sexant (du 29 juillet au 16 août 2007) puis de l’Hydre femelle (du 16 août au 23 août 2007).
En 2014, du 25 au 31 janvier, Vénus fera un court passage dans la constellation de l’Écu, vraisemblablement pour la première fois depuis l’Antiquité. La constellation de l’Écu, autrefois appelée l’Écu de Sobieski, se trouve coincée entre l’Aigle, le Sagittaire et la queue du Serpent.
En 2025, du 22 au 24 mars, elle fera une très courte intrusion dans la constellation de Pégase.

Nouvelles astronomiques

Définition de la parallaxe solaire

Avez-vous déjà entendu parler de la parallaxe solaire ? L'expression peut rebuter, comme d'ailleurs une grande partie du jargon de l'astronome forgé depuis des millénaires. Pourtant, la parallaxe solaire est cette clef qui nous ouvre la connaissance des dimensions et des distances des objets peuplant les cieux. Elle est l'échelle sans laquelle l'homme ne peut se figurer l'Univers. Sa quête – le Graal de l'astronome – débute au IIIe siècle av. J.-C. lorsque l'astronomie se constitue en tant que science. En 1857, l'astronome royal de l'Observatoire de Greenwich, George Bidell Airy, en est encore à qualifier sa détermination de « problème le plus noble de l'astronomie ». Quel est donc ce problème ? Quelle est donc cette parallaxe solaire que tant d'astronomes ont recherchée obstinément à travers les siècles ?

La parallaxe solaire n'est qu'un petit angle insignifiant d'un grand triangle rectangle céleste ayant le rayon de la Terre comme côté opposé et la distance entre les centres de la Terre et du Soleil comme hypoténuse. La connaissance de cet angle fixe donc la distance au Soleil – pourvu que l'on connaisse le rayon terrestre - que l'on nomme glorieusement l'unité astronomique. Toutefois, pour être complètement rigoureux, la parallaxe solaire n'est que la forme abrégée de la parallaxe horizontale équatoriale du Soleil. Compte-tenu de la forme aplatie aux pôles de la Terre, c'est le rayon équatorial qui intervient dans la définition de la parallaxe. Par ailleurs, la distance de la Terre au Soleil varie constamment de sorte que c'est sa valeur moyenne qui est prise en considération. Depuis Kepler, nous savons que la Terre parcourt une trajectoire elliptique autour du Soleil : la distance moyenne va précisément correspondre au demi-grand axe de cette ellipse. Nous connaissons également les distances des différentes planètes au Soleil sous la forme de proportions qui n'ont que peu changées depuis les temps historiques de Copernic et Kepler de sorte que la mesure d'une seule de ces distances donne immédiatement la connaissance de toutes les autres et par conséquent la taille du système solaire.

Les premières mesures de la parallaxe solaire remontent à l'antiquité grecque avec Aristarque de Samos et sa méthode de la dichotomie lunaire, puis Hipparque de Nicée à l'aide des éclipses lunaires. Ils obtiennent une parallaxe de 3' de degré, ce qui revient à placer le Soleil à une distance égale à 1200 rayons terrestres, soit vingt fois inférieure à ce qu'elle est en réalité - une erreur d'une petite seconde de degré revient à déplacer le Soleil de près de 18 millions de kilomètres ! Ça n'est pas rien ; petite erreur, grands effets, ainsi va l'astronomie. La parallaxe du Soleil est en réalité un angle si minuscule que toute mesure non assistée d'un télescope est frappée d'emblée d'une forte imprécision. Cependant, la valeur grecque sera reprise par Ptolémée au IIe siècle après J.-C. qui va, d'une certaine manière, l'officialiser dans sa Grande syntaxe mathématique, encore connue par sa translitération arabe d'Almageste (Al majesti, le très grand). Elle va alors se perpétuer durant 15 siècles jusque dans les années 1620 où un astronome iconoclaste la remettra en question. Dès lors, la recherche de la valeur précise de la parallaxe va reprendre et enflammer l'imagination fertile des astronomes qui, quatre siècles durant, concevront les méthodes et les techniques les plus variées qui les emmèneront dans des expéditions que n'auraient pas désavouées les chevaliers de la Table ronde. C'est en compagnie de ces hommes, leur histoire et leurs méthodes, que nous partirons en 2014 à la recherche de la parallaxe solaire dont Airy nous avertit toujours que « c'est une des [mesures les] plus difficiles à effectuer, et c'est d'elle que dépendent les distances et les dimensions des planètes, des satellites et du Soleil lui-même. »

Année du cheval 馬 (mǎ)

Cette année l'année lunaire (nián : 年) chinoise commence le 31 janvier 2014 et se termine le 18 février 2015. Cette année lunaire est une année embolismique de treize mois lunaires. C'est une année甲午(jiǎ wǔ) qui correspond à la septième branche terrestre 午 (wǔ) associée au signe du cheval 馬 (mǎ) et au premier tronc céleste 甲(jiǎ) associé à l'élément bois 木 (mù). Cette année lunaire contient deux fois le jié qì : lìchūn 立春, début du printemps, cette année est dite double printemps (shuāng chūn : 雙春 [双春]), de même elle contient également deux fois le zhōng qì : yǔshuǐ 雨水, pluie, elle est dite double printemps double pluie (shuāng chūn shuāng yŭ : 雙春雙雨 [双春双雨]).

L'année solaire (suì : 歲 岁) est une année abondante de douze mois lunaires, elle commence au solstice d'hiver (dōng zhì 冬至) du 22 décembre 2013 et se termine au solstice d'hiver suivant (dōng zhì 冬至) du 22 décembre 2014.

	Le calendrier chinois
	Le calendrier 2014 avec quelques explications
	Un calendrier au format A3

Répartition géographique, au 1er mai 2013, en projection de Mercator, du nuage du nuage de débris spatiaux généré par la destruction du satellite Fengyun-1C en janvier 2007

"Gravity" avec ses quatre millions d'entrées en France au box-office est l'un de ces films pour lesquels la "3D" apporte un intérêt incontestable : on prend véritablement conscience des trois dimensions d'espace autour de la Terre, des distances et des vitesses relatives ou absolues ; les rendez-vous spatiaux, en l'occurrence entre les différents astronautes de la mission, se font à des vitesses relatives de quelques mètres par seconde, alors que les vitesses absolues, si l'on représente le mouvement dans un repère lié à la Terre, sont de l'ordre de plusieurs kilomètres par seconde. Très facile de s'imaginer alors l'énergie cinétique mise en oeuvre dans les collisions et les explosions de satellites artificiels. Ceci explique qu'un objet d'une taille centimétrique, pas toujours observable avec les moyens optiques actuels d'ailleurs, peut causer en cas de rencontre malencontreuse avec un satellite opérationnel des dégâts tels que le fonctionnement ou l'existence même de ce satellite peut être remise en cause.

La situation décrite dans le scénario de "Gravity" est somme toute assez fidèle à celle qu'on trouve au-dessus de nos têtes. La population des débris spatiaux est formée d'objets répartis sur différentes trajectoires autour de la Terre (i.e. à différentes altitudes, et à des inclinaisons variées par rapport à l'équateur), avec un nombre total estimé à 35 millions. La majorité de ces objets est de taille submillimétrique, et seulement quelques dizaines de milliers sont observables, et donc catalogués et régulièrement observés ; une grande partie de ces objets est issue de quelques événements catastrophiques dans le voisinage terrestre, telle la collision en février 2009 entre les satellites Cosmos-2251 et Iridium-33, responsable à elle seule d'environ 3000 objets de taille suffisante pour être catalogués, et qui à l'époque avait fait grand bruit (au sol) dans les milieux professionnels concernés. Une autre partie de la population est issue de réactions en chaîne entre débris qui se rencontrent et qui génèrent des objets plus petits : d'une certaine manière, on peut considérer que les débris spatiaux se reproduisent ! Un peu comme les blocs de roche constitutifs des anneaux des planètes géantes qui finissent par produire, en se rencontrant, des objets de toutes tailles. Autour de la Terre également on craint le syndrome de Kessler, scénario de processus de formation en cascade, du nom de l'auteur de plusieurs études sur le sujet depuis les années 1970 à la NASA.

Le mouvement des satellites artificiels et des débris spatiaux est complexe, soumis à de nombreuses forces qu'il faut prendre en compte pour garantir des probabilités de collision compatibles avec l'activité des opérateurs de satellites, voire avec la présence humaine. On pourrait expliquer en raisonnant par ordre de grandeur la plupart des événements du scénario de "Gravity", qui semblent compatibles avec les équations. À part peut-être l'aisance avec laquelle il semble possible de se rendre d'un point A à un point B dans l'espace, sachant que la direction de la vitesse au point A n'a probablement presque jamais rien à voir avec celle de la direction AB, et sachant qu'il n'est possible de la modifier que d'une valeur qui se chiffre en mètres par seconde.

Outre les images magnifiques de l'environnement terrestre offertes par ce film, "Gravity" fait prendre conscience de l'importance de préserver l'espace autour de la Terre, au risque d'être privé, et pour longtemps, des apports des satellites artificiels dans notre vie quotidienne. En particulier au voisinage de l'orbite géostationnaire. Laisser agir le "syndrôme de Kessler" n'est pas une solution, et les scénarios pour y remédier en partie, actuellement à l'étude au sein des agences spatiales, consisteraient à aller rechercher quelques gros objets par année, pour éviter de nouvelles initialisations de ce processus. Des codes de bonne conduite sont désormais imposés aux opérateurs de satellites, et la déclinaison française est la Loi sur les Opérations Spatiales, en vigueur depuis décembre 2010. Elle impose des choix de trajectoires extrêmement stables (à l'échelle de quelques siècles), ou au contraire qui font rentrer les satellites arrivés en fin de vie opérationnelle dans l'atmosphère au bout de quelques années seulement. Le choix de ces orbites "parking" est le fruit d'une longue collaboration entre ingénieurs des agences spatiales et des astronomes, car les lois de la dynamique ne permettent pas tous les scénarios. Il n'est par exemple pas possible de changer à moindre coût l'inclinaison d'une trajectoire par rapport à l'équateur, alors qu'il est très simple d'en changer une altitude.

Ces études à long terme sont l'un des rôles de l'astronomie au service de l'ensemble de la société, et le film "Gravity" vient le rappeler de manière spectaculaire. C'est là une belle mise en scène des applications des mathématiques, des lois de Képler à leurs formes "modernes".

Portrait de Lagrange

Le trimestre thématique Gravasco de l'Institut Henri Poincaré s'est terminé le 6 décembre dernier par une série de commémorations de Michel Hénon et de Joseph-Louis Lagrange.

Ce trimestre qui avait débuté le 9 septembre 2013 par une École d'été au Centre International de Rencontres Mathématiques de Marseille sur le thème des méthodes mathématiques pour la mécanique céleste est de l'avis de tous un grand succès. Quelle récompense pour les organisateurs Jérôme Perez de l'Ensta-Paristech, Stéphane Colombi et Roya Moyahaee de l'Institut d'astrophysique de Paris, Jean-Michel Alimi et Pier-Stéfano Corasaniti du Luth, observatoire de Paris-Meudon.

Revenus à Paris les participants y ont vu se succéder des séries de cours (une trentaine) et de séminaires (une centaine) sur le thème général du problème gravitationnel à N corps pour N variant de 2 jusqu'à l'infini !

C'est tout d'abord la mécanique céleste qui fut mise à l'honneur durant les deux premières semaines coordonnées par Jacques Féjoz (Université Paris Dauphine) sur la théorie KAM puis Alain Albouy (IMCCE, observatoire de Paris) sur l'intégrabilité des problèmes gravitationnels à N corps. La physique statistique des systèmes autogravitants est ensuite devenue le thème d'échange principal entre les participants du 30 septembre au 8 novembre avec deux workshops internationaux et trois séries de cours. Le trimestre s'est ensuite orienté vers les problèmes de structures cosmologiques avec une série de cours et un workshop international (programme détaillé et documents).

Les commémorations finales ont donné l'occasion d'honorer la mémoire de Michel Hénon, illustre astronome, physicien et mathématicien français disparu en avril dernier. Lors de cette commémoration, les travaux scientifiques de ce grand chercheur ont été remémorés par nombre de ses prestigieux collègues internationaux. Sa famille et ses amis se sont aussi rassemblés pour évoquer sa carrière. Une délégation d'une trentaine de participants a même été reçue au Sénat pour un émouvant déjeuner le 5 décembre. Enfin, l'Institut d'astrophysique de Paris a inauguré la salle Michel Hénon afin que sa mémoire reste présente dans l'esprit de tous (détail de ces deux journées).

Le 6 décembre 2013 fut l'occasion de terminer le trimestre par la commémoration du bicentenaire de la disparition de Joseph-Louis Lagrange. Une série de séminaires exceptionnels s'y sont succédé évoquant la biographie générale mais aussi l'œuvre en mécanique céleste de cet illustre maître. Un défilé ouvert par un bataillon d'élèves de l'École polytechnique a donné l'occasion à la centaine de participants d'aller se recueillir devant le caveau de Lagrange au Panthéon. De retour à l'Institut Henri Poincaré, l'occasion a été donnée d'assister en avant-première à la projection du documentaire « Lagrange » réalisé en partie pour l'occasion. Une exposition « Sur les pas de Lagrange » qui s'est tenue du 9 au 19 décembre 2013 à la mairie du 5e arrondissement de la ville de Paris a donné suite à cette journée de commémoration. Le détail de la journée, illustré de nombreuses photos du défilé et du film. Certains éléments de l'exposition peuvent être consultés dans les « images des mathématiques ».

Les organisateurs remercient tous les intervenants du trimestre Gravasco, les nombreux participants, l'Institut Henri Poincaré pour son accueil et l'ensemble de ceux qui ont pu faire de cet intense moment d'échange et de recherche une très belle réussite.

Le patrimoine sort de sa réserve

Évry Schatzman devant le radiotélescope de Nançay

Dès les années 1980, Evry Schatzman avait versé à la Bibliothèque une partie de ses archives. En 2004, un travail plus systématique a permis de reconstituer un fonds complet à partir des versements effectués par lui, des archives conservées dans son bureau, enfin de documents donnés par sa famille. Sa bibliothèque (périodiques, brochures, tirés à part …) a également été concernée. Un travail d'inventaire a été mené parallèlement sous la responsabilité scientifique d'Annie Baglin. Le fonds Schatzman fait actuellement l'objet d'une ultime vérification en vue de la publication en ligne de son inventaire : cet « instrument de recherche » va en effet être encodé en DTD/ead et publié sur la plate-forme Alidade – qui donne accès aux collections patrimoniales de l'Observatoire (http://alidade.obspm.fr/sdx/alidade/) ainsi que sur Calames, catalogue collectif des fonds de manuscrits et d'archives conservés dans les universités et établissements français d'enseignement supérieur et de recherche.

Les archives de l'astrophysicien français (1920-2010) représentent 250 cartons d'archives (soit une trentaine de mètres linéaires) de documents variés et couvrant l'ensemble de sa carrière. Ces archives sont relatives tant à l'activité de chercheur et d'enseignant qu'au militantisme politique et syndical d'Évry Schatzman.

Lire la suite ...

Séminaires