Cette éclipse totale de Soleil est la première de l’année 2024, et sera, comme toujours, l’un des phénomènes célestes les plus spectaculaires à vivre et à observer.

Circonstances générales de l’éclipse

Le tableau ci-dessous donne les circonstances générales de l’éclipse (en UTC). La durée de l’éclipse générale est de 5 h 10 min, la durée de la phase centrale est de 3 h 16 min et sa magnitude est de 1,0579.

Phases	Instant UTC	Longitude λ	Latitude φ
Début de l’éclipse générale (P1)	15 h 42 min	− 143° 06′ 35″	− 14° 57′ 40″
Début de l’éclipse totale (O1)	16 h 38 min	− 158° 12′ 44″	− 8° 02′ 39″
Début de l’éclipse centrale	16 h 40 min	− 158° 32′ 15″	− 7° 49′ 16″
Maximum de l’éclipse (M)	18 h 17 min	− 104° 08′ 37″	25° 17′ 28″
Fin de l’éclipse centrale	19 h 54 min	− 19° 47′ 27″	47° 37′ 10″
Fin de l’éclipse totale (O4)	19 h 55 min	− 20° 08′ 43″	47° 24′ 16″
Fin de l’éclipse générale (P4)	20 h 52 min	− 36° 06′ 15″	40° 33′ 01″

Cette éclipse est visible sur les deux hémisphères terrestres, mais principalement sur l’hémisphère nord. Sa limite boréale passe près du pôle Nord, alors que sa limite australe descend à plus de 38° de latitude sud. Sa bande de totalité traverse une bonne partie de l’océan Pacifique, puis le Mexique, les États-Unis, l’est du Canada et prend fin sur l’océan Atlantique Nord. Elle est visible sous la forme d’une éclipse partielle sur une grande partie de l’Amérique du Nord, sur l’Amérique centrale et sur le nord-ouest de l’Europe (Islande, Irlande, Écosse et Svalbard). Elle est visible sous forme partielle en Polynésie française. Elle est partiellement visible en Guadeloupe, mais à moins de 0,5 % d’obscuration, car très proche de la limite australe de la zone de pénombre.

À travers le portail des formulaires de calcul de l’IMCCE, vous pouvez également obtenir les circonstances locales de l’éclipse, télécharger les cartes de l’éclipse générale et retrouver toutes les éclipses passées et futures. Les résultats sont constamment actualisés en fonction des avancées de la recherche.

Comment observer une éclipse sans danger ?

Que se passe-t-il lors d’une éclipse de Soleil ?

Le Soleil ne peut être éclipsé que dans ses conjonctions avec la Lune (phase de nouvelle lune), celle-ci s’interpose alors entre la Terre et le Soleil. Bien que la Lune soit incomparablement plus petite que le Soleil, elle est cependant suffisamment proche de la Terre pour que son diamètre apparent soit sensiblement égal à celui du Soleil et que l’on puisse observer des éclipses solaires totales.

Si le plan de l’orbite lunaire coïncidait parfaitement avec celui de l’écliptique, nous assisterions chaque mois à une alternance d’éclipses de Soleil et de Lune pour chaque conjonction et chaque opposition de la Lune et du Soleil. Mais du fait de l’inclinaison mutuelle de ces plans, la Lune, dans ses conjonctions et ses oppositions (syzygies), est souvent élevée au-dessus du Soleil ou du cône d’ombre de la Terre, ou abaissée sous le Soleil ou sous le cône d’ombre de la Terre. Elle ne peut recouvrir le Soleil ou passer dans le cône d’ombre de la Terre que si elle se trouve au voisinage de l’un de ses nœuds. Ce qui sera le cas ici.

Pour en savoir plus sur les éclipses et les autres phénomènes d’occultations, explorer ce module interactif.

L’éclipse n’existe effectivement que pour les observateurs situés sur la bande de centralité sur Terre. En dehors de la bande de centralité, mais dans la zone de pénombre, les observateurs verront une éclipse partielle. Pour tout observateur au-delà de cette zone, qu’il soit sur Terre ou ailleurs dans l’espace, la Lune et la Terre n’auront aucune danse commune à présenter.

Que se passera-t-il en Polynésie française ?

Tous les horaires issus de notre documentation sont en UTC, il faut leur retirer 10 h pour être en temps local à Papeete.

Comme nous le voyons dans les circonstances locales propres à Papeete, le phénomène débutera à 5 h 42 heure locale, atteindra son maximum à 6 h 34 et se terminera à 7 h 29. Le Soleil et la lune se levant respectivement à 6 h 07 et 6 h 06, le phénomène suivra le lever du Soleil qui se trouvera temporairement éclipsé par la Lune, comme une course à celui qui se lèvera le premier. La lune se déplaçant, en apparence pour un observateur sur Terre, plus vite autour de la Terre que le couple Terre-Lune autour du Soleil, c’est elle qui gagnera la course, et chacun poursuivra son chemin sur la voûte céleste.

L’observation ne sera cependant pas évidente, et ce pour deux raisons :

• L’éclipse n’étant que partiellement visible depuis Papeete, l’obscuration ne sera que de 60 %, ce qui signifie que la zone ne sera pas plongée pleinement dans l’obscurité. En réalité, la baisse de l’éclat du Soleil, d’à peine 40 %, est trop faible pour que l’on s’en rende compte si l’on ignore qu’une éclipse est en cours.

• L’instant correspondant au lever du Soleil, le phénomène aura lieu à une très faible hauteur au-dessus de l’horizon est, du côté du lever du Soleil. Moins de 6° de hauteur lors du maximum, c’est-à-dire lorsque la baisse de luminosité sera maximale.

C’est donc une éclipse pour les lève-tôt et pour ceux qui pourront monter dans les hauteurs de Tahiti, bien au-dessus de l’horizon local.

Et à Saint-Pierre-et-Miquelon ?

Tous les horaires issus de notre documentation sont en UTC, il faut leur retirer 2 h pour être en temps local à Saint-Pierre-et-Miquelon.

Le phénomène débutera donc à 16 h 36 et terminera à 18 h 47, l’obscuration sera très importante, 98,6 % et le phénomène se situera à 26,25° au-dessus de l’horizon, ce qui promet de belles observations du phénomène !

Pour aller plus loin

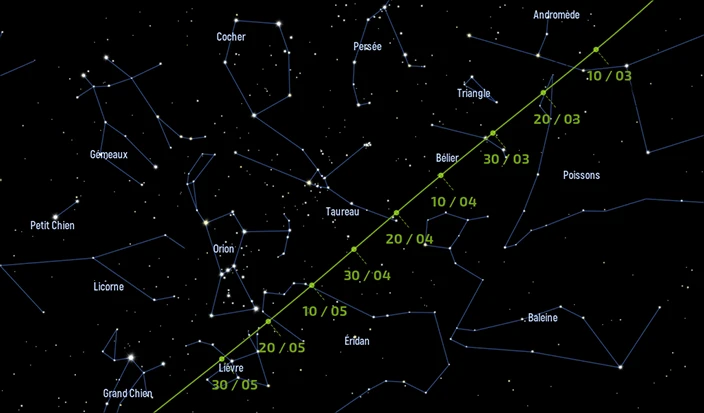
Le maximum de cette éclipse a lieu un jour après le passage de la Lune à son périgée, le diamètre apparent de la Lune (33′ 12,3″) est bien supérieur à celui du Soleil. Il a lieu après le passage de la Lune par son nœud ascendant et peu de temps (3,6 min) avant l’instant de la nouvelle lune. Durant l’éclipse, la Lune se trouve dans la constellation des Poissons.

Voici la suite des événements relatifs à la Lune sur cette courte période de temps.

Série longue de saros contenant cette éclipse

Comme toutes les éclipses de Soleil, cette éclipse est l’un des membres d’une grande famille qui en dénombre 71. Leur caractéristique la plus remarquable réside dans le fait que les éclipses qui composent cette famille sont quasiment identiques. Il y a comme une génétique propre des éclipses qui résulte de coïncidences dans les mouvements célestes qui sont connues depuis l’Antiquité. Elles tiennent en particulier dans le constat simple qu’au bout de 223 lunaisons de 29,53 jours (durée moyenne du mois lunaire entre une nouvelle lune et la suivante), la Lune revient presque exactement à une même position sur son orbite ainsi que vis-à-vis du Soleil. La conséquence est immédiate, si une éclipse survient à une date donnée, une autre éclipse se produira 223 mois (lunaires) plus tard. En outre, cette éclipse sera l’homologue de la précédente au sens où ses caractéristiques générales (type d’éclipse, obscuration, durée…) seront très voisines de la précédente, même si elles évoluent lentement dans le temps. Elles partageront ainsi des traits de famille communs.

Cette période de récurrence de 223 lunaisons – environ 18 ans et 11 jours – porte le nom de saros. Sa reconnaissance dès les temps antiques a permis aux Babyloniens et aux Grecs d’être en mesure de prédire le retour d’une éclipse homologue. Toutefois, le saros seul ne leur permettait pas de prédire de façon précise les lieux sur Terre où il serait donné d’observer l’éclipse. En effet, la période du saros de 223 lunaisons correspond à une durée de 6 585,321 314 jours. Cette durée ne comporte pas un nombre entier de jours écoulés. Si c’était le cas, l’éclipse se reproduirait après un nombre entier de rotations de la Terre et serait donc visible en un même lieu. Au lieu de cela, l’éclipse se déplacera sur Terre en longitude d’environ 120° (1/3 de 360°), ce qui correspond à la partie décimale du saros exprimée en unités angulaires, soit 0,321 314 jour – approximativement 8 h ou 1/3 de jour. Il en découle qu’après 3 saros – cycle de 54 ans nommé exeligmos –, une éclipse homologue reviendra en des lieux très voisins, mais à une date légèrement décalée d’un mois (l’exeligmos est en fait de 54 ans et 32 jours). Nous pouvons le vérifier avec l’éclipse présente dont l’homologue pour une même zone de visibilité sur Terre surviendra le 11 mai 2078.

Cette éclipse appartient à une série longue de saros comportant 71 éclipses homologues successives. La durée de vie d’une telle famille est donc de 1 262 ans. La première éclipse de la famille a pris naissance du côté du pôle Nord le 17 mai 1501. Les éclipses successives descendent lentement vers le pôle Sud où la famille s’éteindra le 3 juillet 2763. Elle se compose de sept éclipses partielles, suivies de onze éclipses hybrides et de quarante-quatre éclipses totales. Puis la série longue se termine avec neuf éclipses partielles. C’est une série très riche en éclipses centrales (55) et pauvre en éclipses partielles (16). L’éclipse du 8 avril 2024 est la trentième éclipse de la série et la douzième éclipse totale.

En tournant autour de la Terre, la Lune passe au cours de sa lunaison de 28 jours devant les étoiles des 13 constellations du zodiaque. Dans la nuit du 22 au 23 avril 2024, la Lune, alors en phase de pleine lune, sera dans la constellation de la Vierge et passera à proximité de la direction de l’étoile Spica qui est la plus brillante de cette constellation. Cette conjonction sera visible toute la nuit.

Qui verra-t-on ?

La Lune est le seul et unique satellite naturel de la Terre. Son diamètre est de 3 474 km (27 % du diamètre terrestre). C’est le cinquième plus gros satellite de notre Système solaire. Elle orbite à une distance moyenne de 384 000 km de la Terre, mais peut s’en approcher à 356 700 km et s’en éloigne au maximum de 406 300 km.

Spica (α Virginis) est l’étoile la plus brillante de la constellation de la Vierge et la quinzième plus brillante (magnitude + 0,97) du ciel. Située à 250 années-lumière du Soleil, il s’agit d’une étoile de type spectrale B, donc massive, chaude et de couleur bleue. Autre caractéristique, c’est une binaire spectroscopique, c’est-à-dire un couple d’étoiles si serré que seul un spectre trahit la présence de deux étoiles.

Que verra-t-on ?

Le rapprochement aura lieu tout au long de la nuit du 22 au 23 avril 2024. Plus on avancera dans la nuit et plus les astres se rapprocheront. La Lune se lèvera la première le 22 avril vers 19 h 40 TLF (Temps légal français), et Spica suivra vers 20 h 05 TLF. Elles seront alors séparées de près de 4° dans le ciel. Les deux astres seront à rechercher sur l’horizon sud-est peu après leurs levers. Vers minuit, l’écart ne sera plus que de 1,5°. Le rapprochement minimum (conjonction) ne sera malheureusement pas visible, puisqu’il aura lieu ce 23 avril vers 6 h 30 TLF avec un écartement de seulement 8′, mais après le coucher des deux astres qui intervient vers 5 h 50 TLF. Toutefois, vers 5 h 30, alors que les astres seront encore visibles au-dessus de l’horizon ouest, l’écartement ne sera déjà plus que d’environ 20′.

L’événement pourra être admiré à l’œil nu, mais tout autant avec des jumelles qui permettront d’admirer une surface lunaire totalement éclairée (pleine lune) et de bien appréhender les mers lunaires. Lors de cette phase de pleine lune, vu depuis la Terre, le sol lunaire est éclairé verticalement, ce qui gomme tous les détails : on ne pourra donc pas voir de cratères comme on peut le faire au moment du premier quartier par exemple. Pour Spica, les jumelles permettront de mettre en évidence sa couleur bleue, couleur bien moins évidente à l’œil nu.

Si le phénomène est banal et fréquent, il aura plusieurs mérites. En premier, celui d’offrir un beau spectacle céleste. Ensuite, celui de mettre en valeur des acteurs très différents : l’un de notre système solaire, et de plus, très proche de nous, et l’autre avec l’une des milliards d’étoiles de notre galaxie et donc située bien au-delà des limites extrêmes du Système solaire. On pourrait rappeler les distances qui nous séparent respectivement, mais ces valeurs ne nous interpelleront pas forcément. Pour mieux appréhender le fossé qui les sépare, amusons-nous avec… la lumière. Rappelons que celle qui quitte le Soleil n’atteint la Terre qu’après un voyage de 8,32 minutes (on dit que la Terre est à 8 minutes-lumière du Soleil). Cela signifie que lorsque l’on regarde le Soleil à midi, on ne le voit pas tel qu’il est à midi, mais tel qu’il était à 11 h 52 (à midi, notre œil reçoit les photons partis du Soleil à 11 h 52). Appliquons cette échelle temps/distance pour les acteurs de notre conjonction du 23 avril : la lumière réfléchie par la Lune parvient sur Terre après un voyage de seulement 1,28 seconde, autant dire quasi instantanément. Par contre, pour Spica, la belle étoile dont la direction frôle la Lune ce soir-là, la lumière aura réalisé un voyage de… 250 ans pour parvenir sur votre rétine.

Mohammad Farhat est libanais. À l’issue d’un master à l’Université américaine de Beyrouth sous la direction de Jihad Touma, il a postulé pour effectuer sa thèse au sein de l’équipe de Jacques Laskar (IMCCE, Observatoire de Paris), connue pour son expertise en mécanique céleste. Il a obtenu une bourse doctorale de Sorbonne Université pour cette thèse. Le sujet initial portait sur les effets de marées dans les systèmes extra-solaires, mais après le démarrage du projet ERC pluridisciplinaire AstroGeo, impliquant géologues et astronomes, il est apparu essentiel de mieux comprendre en tout premier lieu les effets de marées dans le système Terre-Lune. En effet, malgré la proximité de notre satellite, son évolution depuis sa formation restait source de nombreux questionnements depuis cinquante ans.

Depuis les travaux de Georges Darwin en 1880, on sait qu’en raison de l’interaction des marées entre la Terre et la Lune, la rotation de la Terre ralentit et la Lune s’éloigne à raison de 3,83 cm/an. Ceci est mesuré depuis 1969 grâce à la télémétrie laser-Lune avec une précision extrême. L’âge de la Lune est maintenant aussi très bien déterminé à 4,425 milliards d'années. Mais on s’est également rendu compte, depuis plus de cinquante ans, qu’avec le taux de friction de marées actuel, le modèle de marées simple de Darwin conduit à une collision de la Lune avec la Terre il y a environ 1,5 milliard d’années, incompatible avec l’âge de la Lune.

Au cours de son travail de thèse, Mohammad Farhat a élaboré le premier modèle physique cohérent, permettant de rendre compte à la fois de la récession actuelle de la Lune et de son âge. Ce travail a nécessité la prise en compte de plusieurs éléments, dont le premier est l’étude des marées océaniques. On sait depuis longtemps que la source principale de dissipation se produit dans les océans, et non dans la Terre solide. La dissipation de marée pour la planète Mars, par exemple, qui ne possède pas d’océan, est dix fois moindre que celle de la Terre. Les travaux de Webb (1982) ont montré la présence de résonances dans ces effets de marées océaniques. Pour certaines valeurs de la vitesse de rotation de la Terre, ces résonances entre le forçage de marée, lié à la durée du jour, et les oscillations propres de l’océan, peuvent entraîner une amplification de la dissipation de marée. En particulier, nous sommes actuellement proches d’une telle résonance. La dissipation est alors amplifiée, et était donc plus faible dans le passé. Reste à construire un scénario cohérent de l’évolution du système Terre-Lune.

La plupart des travaux récents s’appuyaient sur les indicateurs géologiques, témoins de la vitesse de rotation passée de la Terre. Cependant, la précision de ces données est très difficile à estimer, et certaines ne sont pas cohérentes entre elles. Dans le cadre de cette thèse, il a donc été décidé de ne pas tenir compte, en un premier temps, des données géologiques, et de ne considérer que les données extrêmement bien déterminées que sont l’âge de la Lune et sa vitesse de récession actuelle. Pour établir son modèle, Mohammad Farhat a pu s’appuyer sur les développements analytiques effectués par Pierre Auclair-Desrotour (IMCCE/Observatoire de Paris) dans ces dernières années. Le modèle utilisé est très simple, et considère une Terre, soit formée d’un océan global, soit constituée d’un océan hémisphérique, et d’un continent occupant l’hémisphère complémentaire. Mohammad a aussi introduit une évolution moyenne des continents, en se reposant sur ce qui est connu sur l’évolution de la tectonique des plaques au cours du dernier milliard d’années.

L’intérêt d’un tel modèle simple (dans son expression, car la réalisation reste extrêmement complexe) est de ne posséder que deux paramètres libres : la profondeur océanique et un paramètre de dissipation au fond des océans. L’ajustement de ces paramètres aux deux données connues (vitesse de récession et âge de la Lune) a alors permis d’obtenir un modèle unique. Une fois obtenu, ce modèle a été comparé aux observations géologiques disponibles. L’accord de ces données avec le modèle de Mohammad Farhat est impressionnant. On obtient ainsi, pour la première fois, un modèle de l’évolution du système Terre-Lune cohérent avec la récession actuelle de la Lune et avec l’âge de la Lune, et qui, de plus, s’accorde avec les données géologiques les plus fiables. Ce modèle a reçu un accueil très positif de la part de la communauté des géologues, et sert dès à présent de référence pour les études sur les sédiments anciens, études dont le nombre va croissant.

Après sa thèse soutenue le 5 janvier 2023, Mohammad Farhat a continué son travail sur la dissipation dans le système Terre-Lune en tant que postdoctorant à l’IMCCE au sein du projet ERC AstroGeo (www.astrogeo.eu). Il vient d’obtenir une Miller Fellowship à l’Université de Berkeley (https://miller.berkeley.edu/fellowship), CA, USA, qu’il rejoindra à l’automne 2024.

Depuis début mars, elle a atteint une magnitude de 6, soit la limite pour la voir à l’œil nu dans un ciel de qualité loin de la pollution lumineuse des villes (voir figure en entrée d’article). Il est recommandé de l’observer au moins avec des jumelles, voire avec un petit télescope.

Cette comète, dont l’orbite est très inclinée (74°), est probablement issue du nuage de Oort. Elle revient dans le Système solaire interne avec une périodicité d’environ 71 ans. Elle est connue pour avoir des sursauts fréquents de dégazage lors de ses passages au périhélie. Des images de structures autour du noyau ont pu être faites au télescope de 1 m du pic du Midi (figure ci-dessous). Ces structures en spirale sont la conséquence de jets de dégazage avec un noyau en rotation.

La comète reste observable en ce début avril en regardant vers l’ouest après le coucher du Soleil, en direction de la galaxie d’Andromède, puis progressivement en direction de la constellation du Bélier (voir figure ci-dessous). Passant au périhélie le 21 avril prochain, elle commencera à disparaître dans les lueurs du crépuscule aux alentours du 10 avril. La comète passera au plus proche de la Terre le 2 juin, date après laquelle elle deviendra visible depuis l’hémisphère sud.