A consistent scenario for the evolution of the Earth-Moon distance
Due to tidal friction, the Earth’s rotation slows down and the Moon goes away.
This is measured with centimetre precision using Lunar Laser ranging. But up to now, there was no physical model that accounts for both this measured tidal dissipation and the age of the Moon. The IMCCE research team has elaborated a physical model of the Earth-Moon orbital evolution that perfectly agrees with these constraints, and also to the available geological records, solving a fifty-year-old paradox. This study is published in A&A Letters.

Since the work of Georges Darwin, 1880, it is known that due to the tidal interaction between the Earth and the Moon, the Earth’s spin slows down and the Moon goes away. This has been measured first with ancient eclipses, and since 1969 with Lunar Laser ranging, reaching extreme accuracy at 3.83 cm/year. The age of the Moon is now also very well determined at 4.425 Ga. But it has also been realised, more than fifty years ago, that the simple tidal model of Darwin, starting with the present tidal rate, leads to a collision of the Moon with the Earth at about 1.4 Ga (Gerstenkorn event), incompatible with the known age of the Moon.
Since then, a lot of work has been devoted to the resolution of this paradox. The ocean models of Webb (1982) provided fundamental progress, showing the occurrence of tidal resonances leading to a large increase of the tidal dissipation in these resonant states. One could thus think that we are at present in a resonant state, with anomalous high dissipation. Nevertheless, this model did not fit either the present tidal rate or the age of the Moon.
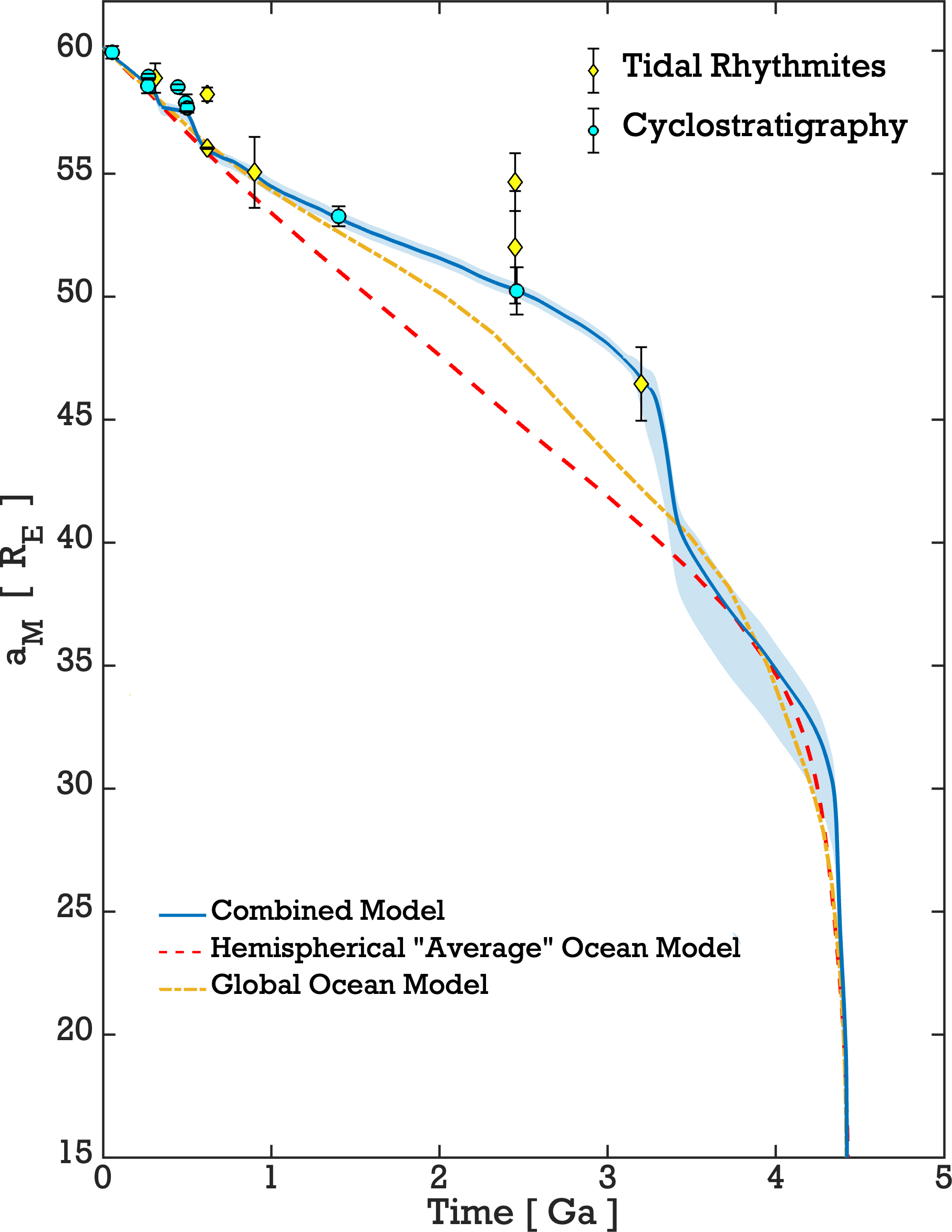
For the data, several stratigraphic sequences have been considered to record the past rotation state of the Earth. Among them, the tidal rhythmites, related to the variation of the tidal deposition between neap and spring tides, or the cyclostratigraphic records which allow deriving the Earth precession rate from the Milankovitch cycles record. Nevertheless, the adequate sequences are still rare and their interpretations often controversial. In some cases, various groups analysing the same data reach incompatible results. Still, these data are used for the establishment of empirical models of the Earth-Moon history that are widely used today by geologists. As the geological data are used to establish the models, it is difficult to avoid circular arguments. Moreover, little physical insight is gained with these empirical models.
On the other hand, there has been recently quite an activity on the theoretical tidal models, with the elaboration of numerical model whose main objective is to fit the geological data, but up to now, these models fail to match the age of the Moon.
The approach of the research team from IMCCE (CNRS, Observatoire de Paris, University PSL, Sorbonne Université) is different. They deliberately avoided to take into account the geological data as they wanted a model that would be free from any circular reasoning. They considered an analytical model, similar to (Webb, 1982), but more refined, with a hemispheric continent that evolves backward in time towards a global ocean, taking into account the plate tectonic reconstruction in the first Ga. This induces a non-trivial analytic treatment that takes into account the continental drift. Still, this model has only two parameters, as in (Webb, 1982), or (Tyler, 2021). An exploration of the parameter space and a search for the best fit to the present rate of tidal dissipation, and the age of the Moon leads to a single solution, fitting these constraints extremely well.
This single solution agrees very well with most of the relevant geological data (In Fig.1, all available data are plotted, without any selection). Two points are of particular interest as they are obtained with careful cyclostratigraphic analyses: (Meyers and Malinverno, PNAS, 2018) at 1.4 Ga, and (Lantink et al., PNAS 2022) at 2.46 Ga. The agreement with those data points is amazing.
This study is interdisciplinary and will have a broad impact in several fields (geophysics, geology, astronomy). It provides the first physical model of the Earth-Moon evolution that perfectly agrees with the present tidal dissipation and the age of the Moon, solving a fifty-year-old paradox. Moreover, this model fits very well with the available geological data. It will thus most probably become the standard reference for geoscientific studies. This study demonstrates that the cyclostratigraphic approach is very relevant for retrieving the past rotational state of the Earth and should consolidate the whole cyclostratigraphic field. This model differs from the previously published ones by allowing resonances of larger amplitudes. This is essential in the fit of the present dissipation rate. This result will thus also consolidate the oceanic tidal theory, showing the important effect of the oceanic resonances. Furthermore, it can be generalised to oceanic tides in extrasolar planets.
This work was supported by the ANR AstroMeso and the ERC AstroGeo.
Reference
M. Farhat, P. Auclair-Desrotour, G. Boué, J. Laskar, 2022, « The resonant tidal evolution of the Earth-Moon distance », A&A Letters.
Contacts researchers
- Jacques Laskar, CNRS research director, IMCCE/Observatoire de Paris,
Jacques.Laskar@observatoiredeparis.psl.eu - Mohammad Farhat, PhD student, IMCCE/Observatoire de Paris,
Mohammad.Farhat@observatoiredeparis.psl.eu