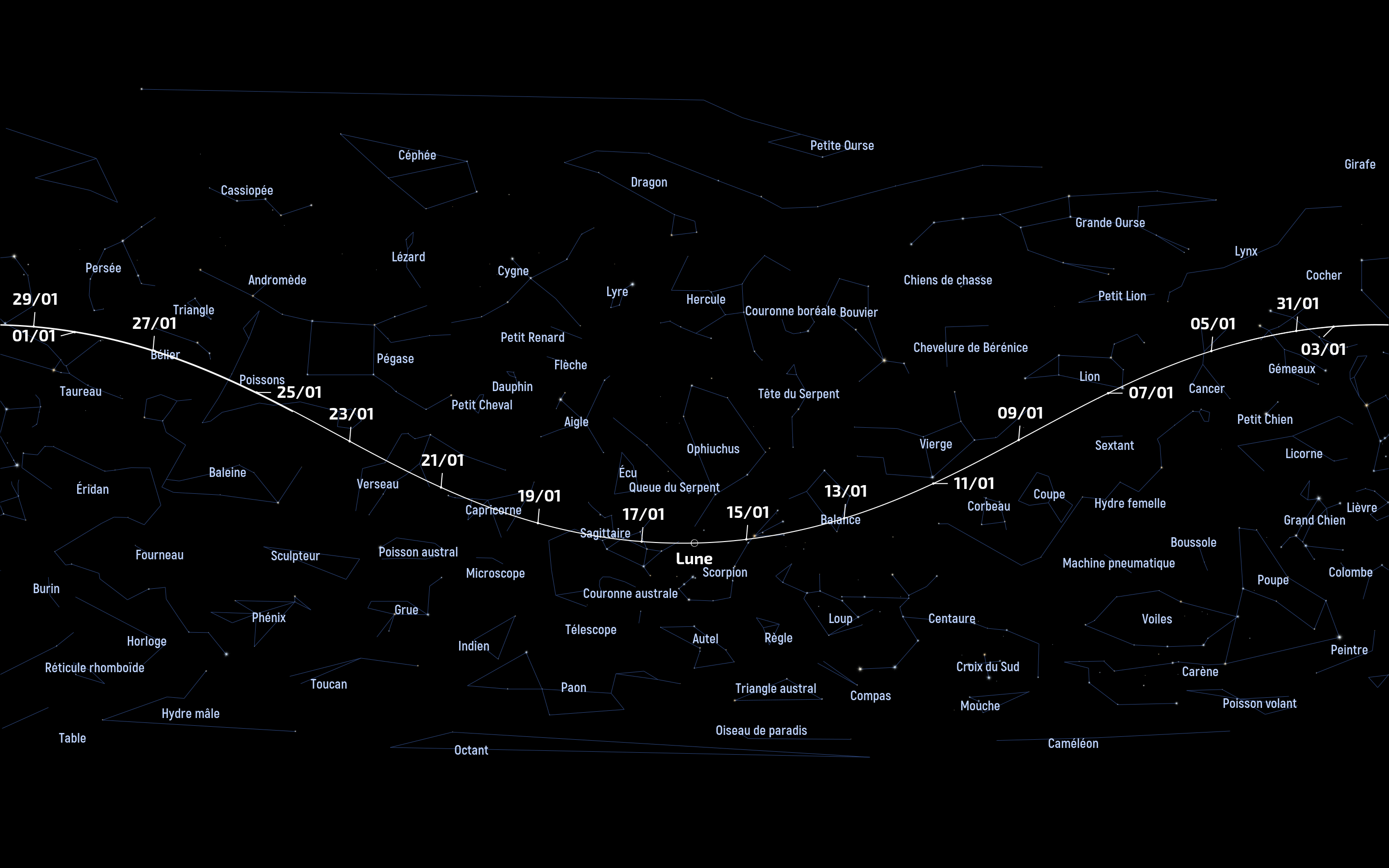
Nul doute que le spectacle attirera du regard même les moins intéressés par ce qui se passe dans le ciel puisqu'il sera difficile de ne pas les voir.
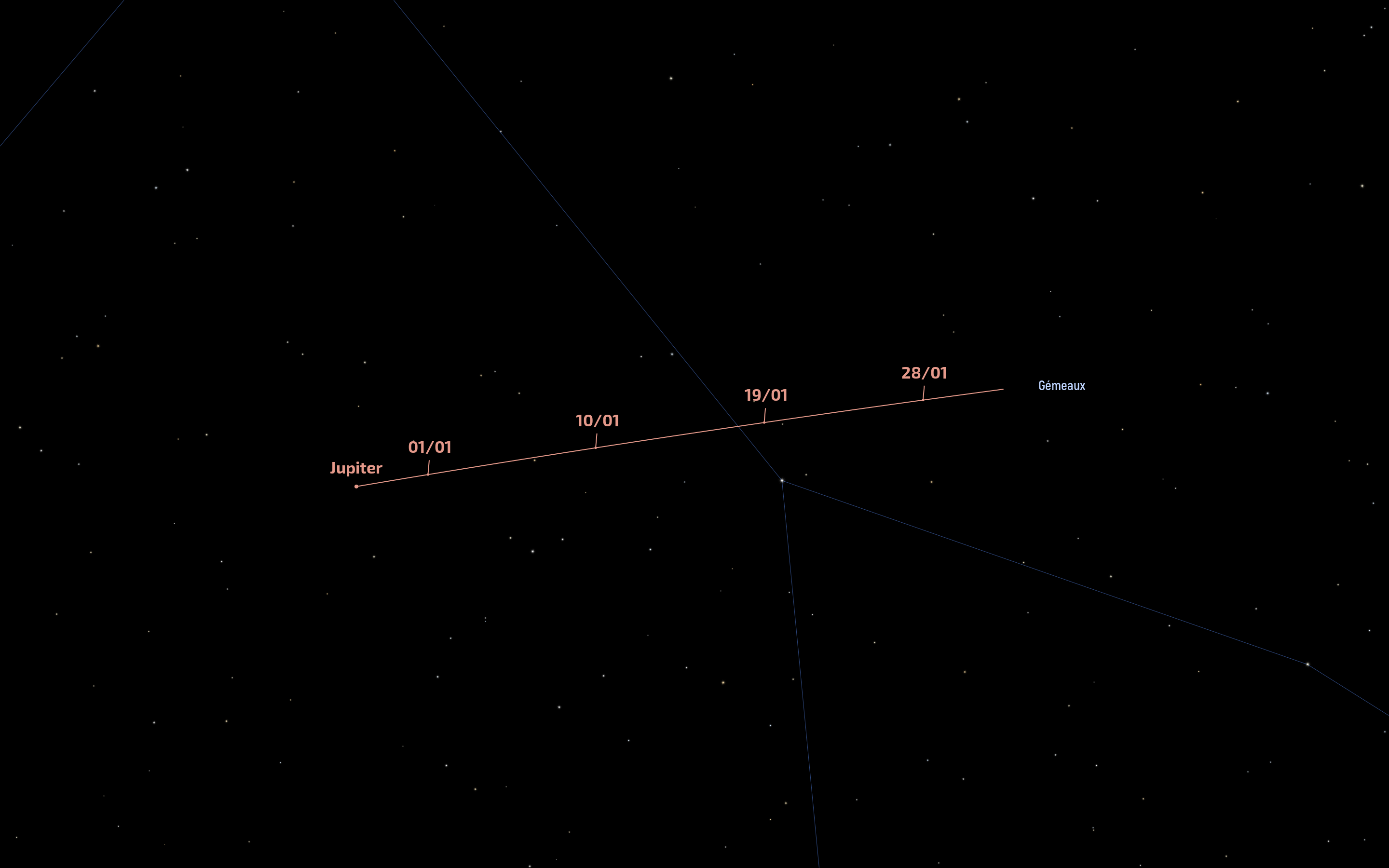
Le hasard de la mécanique céleste veut en effet que lors de sa phase de pleine Lune de janvier 2026, la Lune passera 3,5 degrés au nord (au-dessus) de Jupiter qui brillera à la magnitude - 2,7 soit proche de son plus grand éclat possible. Il se trouve que du fait d'un autre heureux hasard, Jupiter sera non loin de son opposition de 2026 qui aura lieu de 10 janvier.
La conjonction géocentrique en longitude aura lieu à 23 h 54 TLF. La différence de latitudes géocentriques sera de 3°37´13,1″ et l’élongation géocentrique minimum aura lieu le 4 janvier à 0 h 14min et elle sera de 3°36´51,9".
Que verra-t-on ?
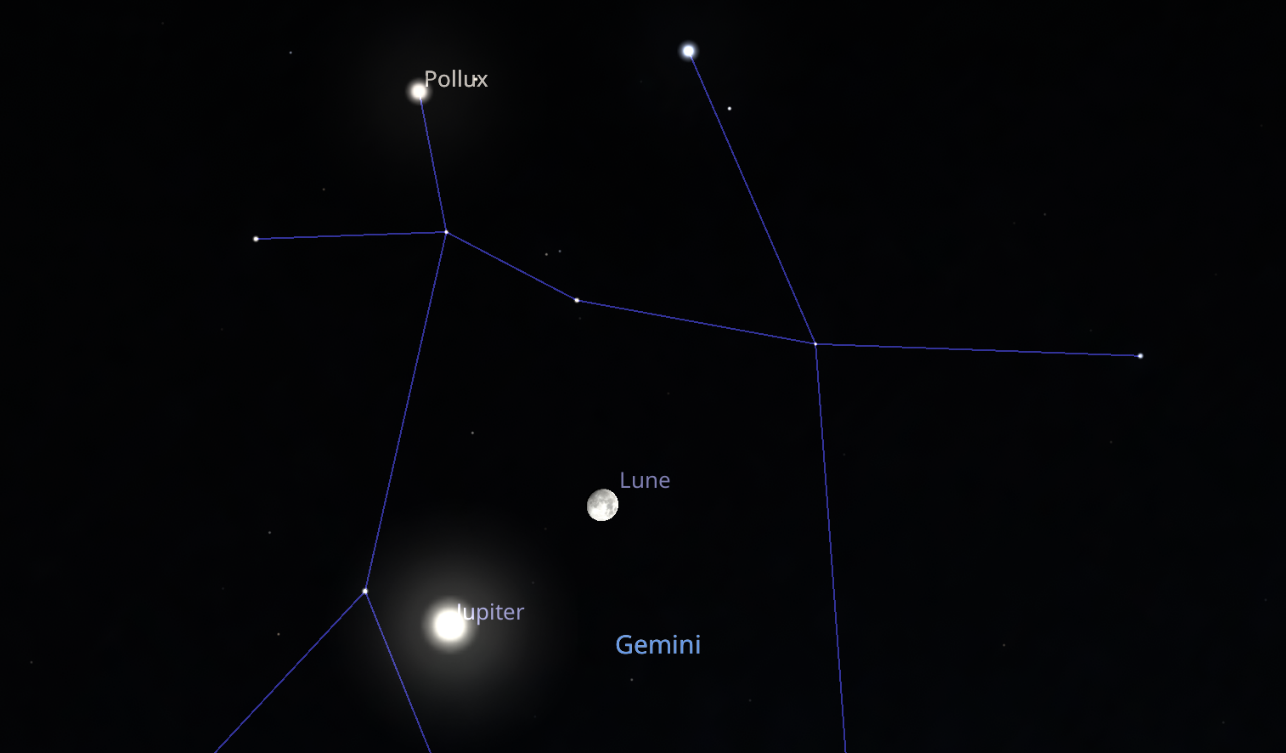
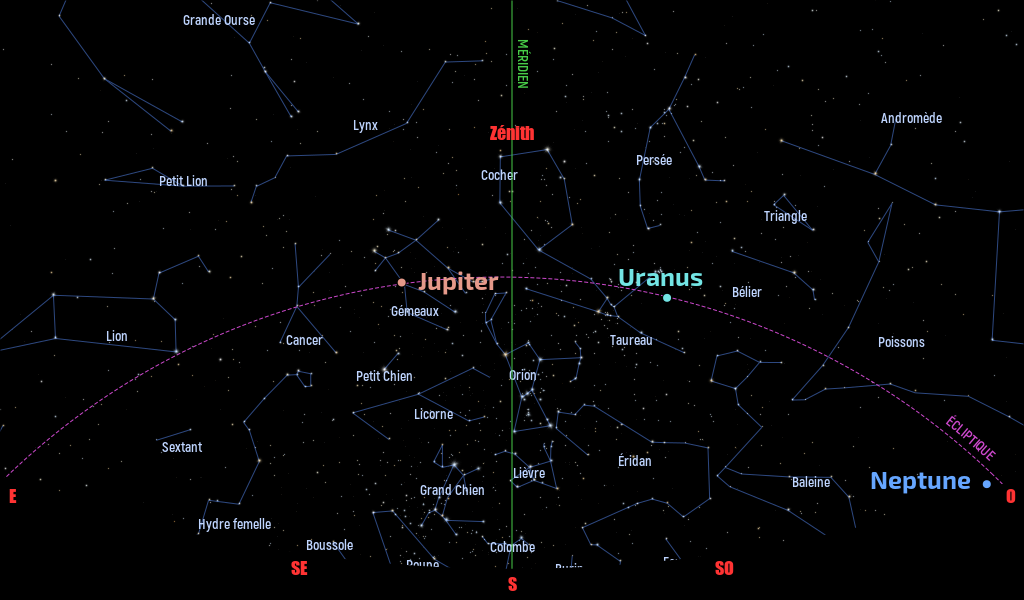
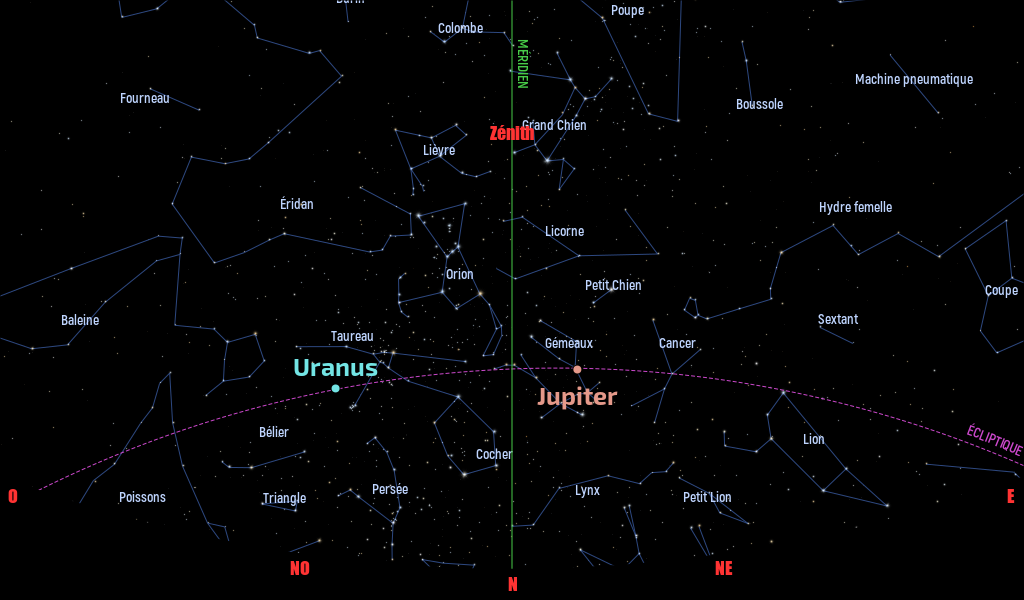
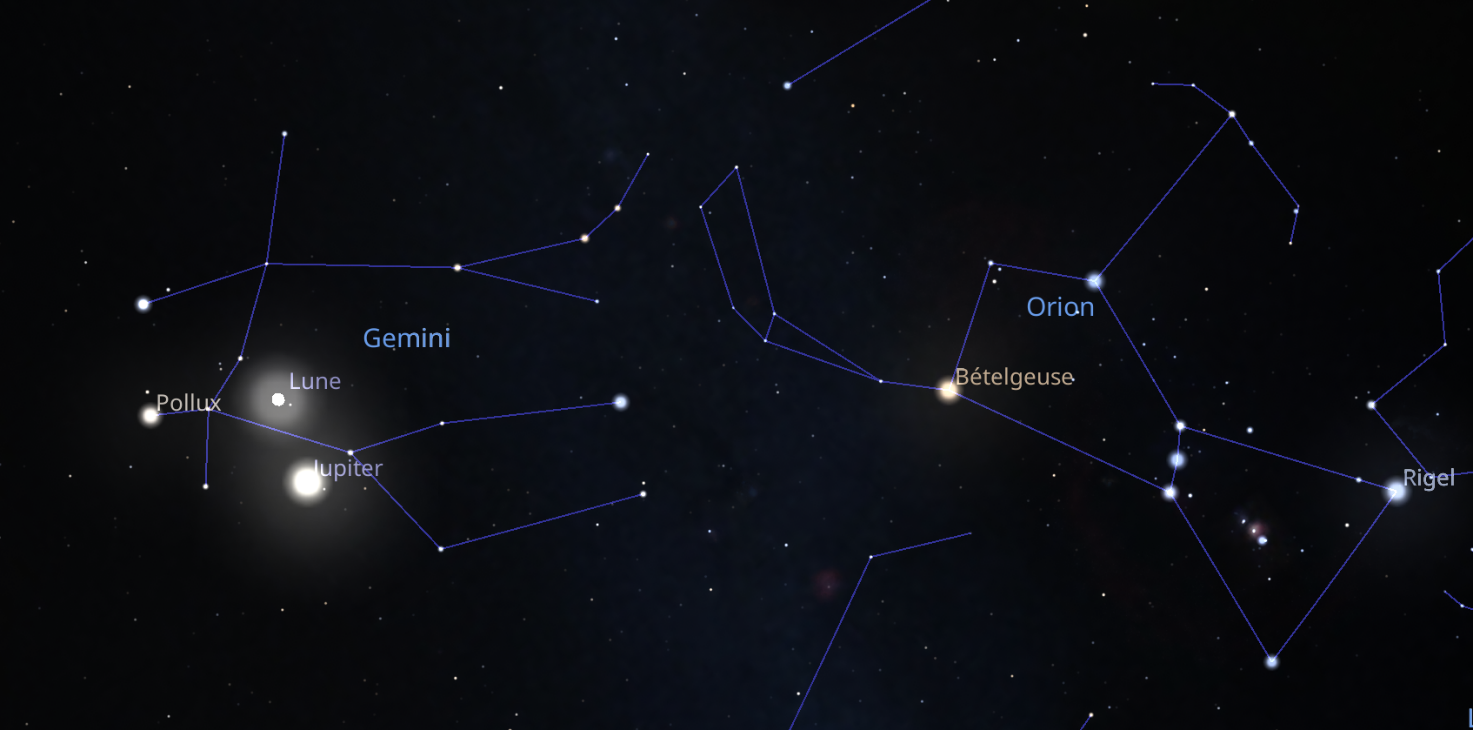
Dans la nuit du 3 au 4 janvier 2026, les deux astres, qui seront situés dans la constellation des Gémeaux, se lèveront vers 17 h 30 vers le nord-est alors que, à l'opposé s'estomperont les dernières lueurs du couchant au-dessus de l'horizon sud-ouest. Vers 19h, Jupiter sera positionnée 12° au-dessus de l'horizon alors que la Lune sera quant à elle à 17° de ce même horizon.
On sait que la pleine Lune est visible tout au long de la nuit puisqu'elle se lève en même temps que le Soleil se couche et qu’elle se couche en fin de nuit lorsque le Soleil se lève. De ce fait, la conjonction sera donc visible tout au long de la nuit. Les deux astres passeront le méridien sud vers 1 h 30 min TLF ; ils seront alors très haut dans le ciel, à 65° au-dessus de l'horizon.
La distance Terre-Lune sera cette nuit-là d'environ 364 000 km. Sachant que l'apogée (plus grande distance à la Terre le 13 janvier) est de 405 438 km et que le périgée (plus courte distance) est de 360 347 km, on comprendra que la Lune sera à une distance parmi les plus proches. C'est ce qui explique son diamètre assez conséquent de l'ordre de 32'54".
Jupiter, quant à elle, sera distante de 4,27 ua soit environ 634 millions de km. La proximité de son opposition une semaine plus tard explique son diamètre apparent proche de 47''.
Pour l'observation du phénomène, point n'est besoin d'un instrument : l’œil nu conviendra parfaitement. On remarquera comme sur la figure ci-dessous que les deux astres sont situés à l'ouest (à droite) de la célèbre étoile Pollux.
Un instrument sera toutefois intéressant pour profiter de Jupiter et de son diamètre important. Notons tout d'abord que les quatre satellites galiléens seront tous disposés du même côté du disque jovien.
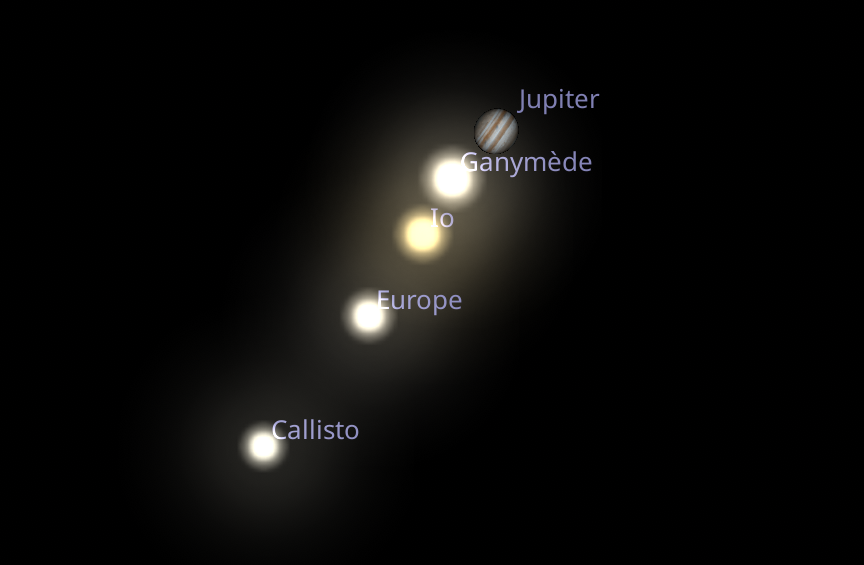
Ensuite, la taille conséquente offerte par la proximité de l'opposition permet de mieux détailler sa surface. Ce soir-là offrira par exemple une autre belle opportunité dans un créneau horaire pratique : la grande tache rouge sera au méridien central à 22h27 TLF.

Pour la Lune par contre, un instrument ne sera que de peu d'utilité. Lors d'une phase de pleine Lune, le sol lunaire est violemment éclairé ; le disque est aveuglant et sans aucun détail car, éclairé verticalement, aucun relief ne projette d'ombre.
Dans la nuit du 30 au 31 janvier 2026, le phénomène se produit quasi à l'identique. La conjonction géocentrique en longitude aura lieu à 4 h 18 TLF le 31 janvier. La différence de latitudes géocentriques sera de 3°47´24,1" et le minimum d’élongation géocentrique aura lieu à 4 h 39 et sera de 3° 47´ 2,7" :