Shedding new light on planetary chaos
The question of the stability of the solar system arose since the enunciation of the law of universal gravitation by Newton. Newton’s law allows to recover Kepler’s fixed ellipses for a single planet around the sun, Jupiter, for example. But as soon as we consider a second planet, Saturn, the law also announces that Saturn disturbs the orbit of Jupiter. The big question, which Newton already poses in the preface to his optical volume (1706), is then whether these disturbances between the planets will destabilize the system. This problem will be solved in a first approximation by Laplace and Lagrange at the end of the 18th century. Laplace shows that the size of planetary orbits is invariant on average. Lagrange introduces the formalism that allows him to calculate their long-term evolution. Planetary ellipses rotate slowly in their plane and in space, with notable variations in their eccentricity and inclination, but which do not allow planetary collisions. The system is stable and predictable over an infinite time. This triumph was of short duration, because at the end of the XIXth century, Henri Poincaré shows that the problem of the three bodies is not integrable. He highlighted the zones that are now called chaotic, in which the orbits can show a very high sensitivity to their initial conditions. After Poincaré, mathematicians and astronomers continued their quest for stability for the solar system. The famous KAM theorem (Kolmogorov, Arnold, Moser) shows that despite the areas of instability highlighted by Poincaré, there remains a large number of regular solutions provided that the planetary masses are small enough. The application of this result to the motion of the planets by Vladimir Arnold in 1963 will again be considered as a proof of the stability of the solar system, even if Michel Hénon then pointed out that its application requires planetary masses much lower than the mass of the electron.
More than thirty years ago, using computer algebra methods coupled with numerical integrations, Jacques Laskar (Institut de mécanique céleste et de calcul des éphémérides (IMCCE), CNRS, Observatoire de Paris, Université Paris Sciences et Lettres) showed that the motion of the planets in the solar system is chaotic and not regular, as had been widely assumed until then. One of the first outcomes of this result is the impossibility of predicting the movement of the planets in the solar system over a period of more than 60 million years (Ma). The uncertainty on the trajectories of the planetary orbits diverge exponentially with a characteristic time of 5 Ma. In other words, this uncertainty is multiplied by 10 every 10 Ma. This limits the possibilities of calculating variations in insolation on the Earth’s surface resulting from variations in the Earth’s orbit, themselves due to disturbances from other planets. This then also limits the possibility of establishing geological time scales based on the correlation between the sedimentary series which testify of the climatic variations of the past and the insolation computations of celestial mechanics. Over longer periods of the order of the age of the solar system, the planets can even collide, among themselves or with the sun, with, for Mercury, a probability of collision of the order of 1%.
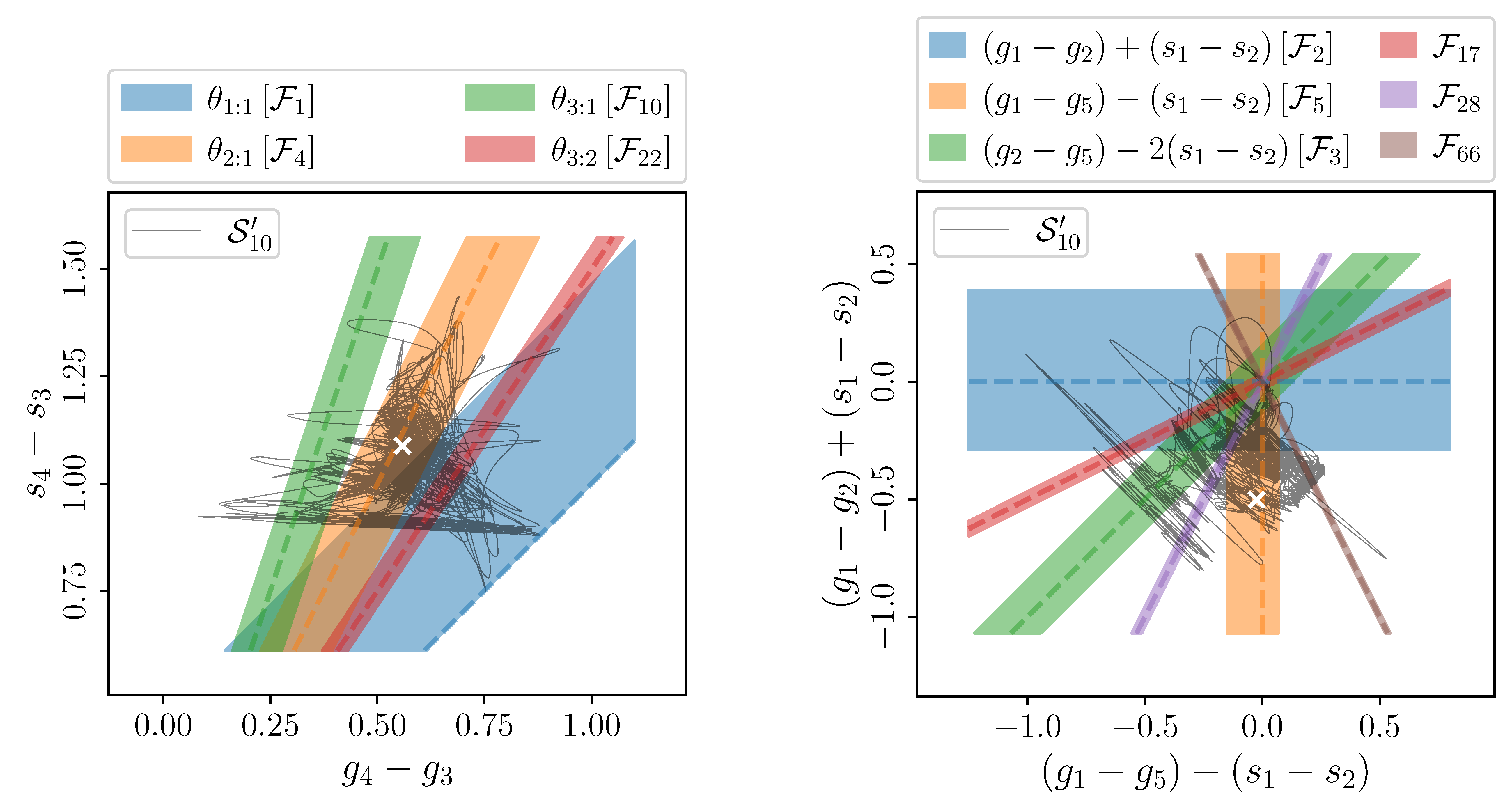
These results are now well accepted, but the origin of this chaotic motion remained a source of controversy. J. Laskar had highlighted a major role played by two resonances between the precessional movements of the planetary orbits. One involving the modes associated with the planets Mercury, Venus, Jupiter ((g1-g5)-(s1-s2)), and another linked to Earth and Mars (2(g4-g3)-(s4-s3)). The latter had been challenged by American researchers when they had reproduced the results of J. Laskar through numerical calculations on computers. Since then, these doubts have been taken up in the scientific literature until very recently. On the other hand, no one has so far reproduced the analytical calculations that led to the discovery of the chaotic motion of the planets.
To put an end to this controversy, Federico Mogavero and J. Laskar used the computer algebra software TRIP (www.imcce.fr/trip) developed over thirty years within the IMCCE team, to conduct a systematic study of all the resonances present in the inner solar system. These calculations, which have just been published as a Letter in the journal Astronomy & Astrophysics, involve developments of several million analytical terms. After analysis, these terms are classified by decreasing amplitude. Among the very first, we find the resonances discovered thirty years ago by J. Laskar. At the same time, a multidimensional network of new resonances, strongly coupling the inner planets, is revealed. The researchers show that taking into account the most important resonances of this network makes it possible to account for the characteristic time of 5 Ma for the exponential divergence of the planetary orbits. The application of computer algebra at the basis of this study has therefore made it possible to overcome the great complexity of the dynamics of the planets, by revealing the entanglement of resonances which is the source of the chaotic behavior of their orbits.
In a joint study of more than 100,000 solutions, the IMCCE team also confirms that the probability of collision of Mercury over 5 billion years (Ga) is indeed of the order of 1%. This probability reaches more than 90% if these calculations are extended over 100 Ga, forgetting that the life expectancy of the sun is probably only 5 Ga.
References
- F. Mogavero and J. Laskar, “The origin of chaos in the Solar System through computer algebra”, Astron. Astrophys. Letters, in press, DOI: https://doi.org/10.1051/0004-6361/202243327.
- N.H. Hoang, F. Mogavero, J. Laskar, “Long-term instability of the inner Solar System : numerical experiments”, MNRAS, in press, DOI: https://doi.org/10.1093/mnras/stac1299.
Contacts researchers
- Jacques Laskar (IMCCE/
Observatoire de Paris – PSL),
Jacques.Laskar@observatoiredeparis.psl.eu - Federico Mogavero (IMCCE/
Observatoire de Paris – PSL),
Federico.Mogavero@observatoiredeparis.psl.eu